COMPARING FRACTIONS
Lesson 23 Section 2
The ratio of two fractions
To know the ratio of fractions, is to compare them. We are about to see:
Fractions have the same ratio to one another as natural numbers.
If you knew that
| 2 3 |
is to | 5 8 |
as | 16 is to 15, |
| then since 16 is larger than 15, you would know that | 2 3 |
is larger than | 5 8 |
. |
Now we saw in Lesson 20 that when two fractions have equal denominators, then the larger the numerator, the larger the fraction.
| 2 5 |
is larger than | 1 5 |
. |
| But what specifically is the ratio of | 2 5 |
to | 1 5 |
? |
| 2 5 |
is to | 1 5 |
as 2 is to 1. |
| 2 5 |
is two times | 1 5 |
. |
In other words:
Fractions with equal denominators are in the same ratio
as their numerators
| 2 5 |
is to | 3 5 |
as 2 is to 3. |
When fractions do not have equal denominators, then we can know their ratio -- we can compare them -- by cross-multiplying. Because that gives the numerators if we had expressed them with equal denominators.
| 4. | How can we compare fractions by cross-multiplying? |
| Cross-multiply and compare the numerators. | |
| Example 1. | 2 3 |
is to | 5 8 |
|
| as | 2 × 8 | is to | 3 × 5 | |
| as | 16 | is to | 15. | |
| 16 and 15 are the numerators we would get if we expressed | 2 3 |
and | 5 8 |
with the common denominator 24.
as
| 16 24 |
is to | 15 24 |
. |
| And since 16 is larger than 15, we would know that | 2 3 |
is larger than | 5 8 |
. |
| Example 2. Which is larger, | 4 7 |
or | 5 9 |
? |
Answer. On cross-multiplying,
| 4 7 |
is to | 5 9 |
as
36 is to 35.
36 is larger than 35. Therefore,
| 4 7 |
is larger than | 5 9 |
. |
Note: We must begin multiplying with the numerator on the left:
4 × 9.
| Example 3. | 1 4 |
is to | 1 2 |
as which whole numbers? |
Answer. On cross-multiplying,
| 1 4 |
is to | 1 2 |
as
2 is to 4.
That is,
| 1 4 |
is half of | 1 2 |
. |
Example 4. What ratio has 2½ to 3?
| Answer. First, express 2½ as the improper fraction | 5 2 |
. Then, treat the |
whole number 3 as a numerator, and cross-multiply:
| 5 2 |
is to 3 as 5 is to 6. |
2½ is five sixths of 3.
| Equivalently, since 3 = | 6 2 |
(Lesson 21, Question 2), then |
| 5 2 |
is to | 6 2 |
as 5 is to 6. |
In general:
To express the ratio of a fraction to a whole number,
multiply the whole number by the denominator.
| 6 7 |
is to 3 as 6 is to 21. |
For an application of this, see Lesson 26.
| Example 5. On a map, | 3 4 |
of an inch represents 60 miles. How many |
miles does 2 inches represent?
Solution. Proportionally,
| 3 4 |
of an inch is to 2 inches as 60 miles is to ? miles. |
| What ratio has | 3 4 |
to 2? |
| 3 4 |
is to 2 as 3 is to 8. |
Therefore:
3 is to 8 as 60 miles is to ? miles.
Since 20 × 3 = 60, then 20 × 8 = 160 miles.
The theorem of the same multiple.
Or, inversely:
8 is to 3 as ? miles is to 60 miles.
Now,
8 is two and two thirds times 3.
(Lesson 18, Example 5.) Therefore, the missing term will be
| Two and two thirds times 60 | = | Two times 60 + two thirds of 60 |
| (Lesson 16) | ||
| = | 120 + 40 | |
| = | 160 miles. | |
More than or less than ½
| 5. |
How can we know whether a fraction is more than or less than ½? |
| If the numerator is more than half of the denominator, | |
|
|
|
| then the fraction is more than ½. While if the numerator is less than half of the denominator, | |
|
|
|
| the fraction is less than ½. | |
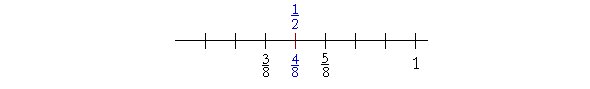
| 4 8 |
is equal to | 1 2 |
, because 4 is half of 8. Therefore, | 5 8 |
is more than | 1 2 |
, |
| because 5 is more than half of 8; while | 3 8 |
is less than | 1 2 |
, because 3 is less |
than half of 8.
| Example 6. Which is larger, | 7 12 |
or | 9 20 |
? |
| Answer. | 7 12 |
. Because 7 is more than half of 12, while 9 is less than half |
of 20.
| Example 7. Which is larger, | 11 21 |
or | 12 25 |
? |
| Answer. | 11 21 |
. Because 11 is more than half of 21 (which is 10½); while 12 |
is less than half of 25 (which is 12½). (Lesson 16, Question 8.)
We could make these comparisons for any ratio of the terms. For example, we could know that
| 5 15 |
is larger than | 6 21 |
. |
Because 5 is a third of 15, but 6 is less than a third of 21 (which is 7).
Example 8 Which is the largest number?
| 3 10 |
5 8 |
1 2 |
2 7 |
5 9 |
Answer. First, let us examine the list to see if there are numbers less than ½ or greater than ½. We may eliminate any numbers less than (or equal to) ½.
| And so we may eliminate | 3 10 |
, | 1 2 |
, and | 2 7 |
. |
| We are left with | 5 8 |
and | 5 9 |
. |
Since the numerators are the same (Lesson 20, Question 11), we
| conclude that the largest number is | 5 8 |
. |
Example 9. Which is the largest number?
| 5 9 |
2 5 |
6 11 |
| Answer. We may eliminate | 2 5 |
because it is less than ½, while the others |
are greater. Which is larger, then,
| 5 9 |
or | 6 11 |
? |
On cross-multiplying, we have 5 × 11 versus 9 × 6. And
55 is greater than 54.
Therefore,
| 5 9 |
is greater than | 6 11 |
. |
Please "turn" the page and do some Problems.
or
Continue on to the next Lesson.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
