Lesson 12
SHORT DIVISION
Division is the inverse of multiplication; therefore it depends on knowing the multiplication table.
The problem of division is to find what number times the Divisor will equal the Dividend. That number is called the Quotient. (Lesson 11.) To find the quotient, there is a method called short division.
In this Lesson, we will answer the following:
- When we write the division box, where do we write the divisor?
- How do we do short division?
- How do we proceed when the dividend is a decimal?
- How do we round off, or approximate, a decimal to a given number of decimal digits?
- How do we express the quotient as a decimal?
- How do we proceed when the dividend is less than the divisor?
- Calculator problems

Dividend ÷ Divisor = Quotient
Quotient × Divisor = Dividend
Example. Using the division box, write 1 ÷ 5. (There is nothing to calculate.)
Answer. 5 is the divisor. It goes outside the box.
![]()
Before going on to short division, the student should be clear about division with remainder, and how to name the remainder. See Example 11 of that Lesson.
| 2. | How do we do short division? |
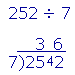
|
|
|
From the left of the dividend (252), take as many digits as necessary to form a number (25) that will contain the divisor (7) at least once but less than ten times. Divide that partial dividend by the divisor, and obtain the first digit of the quotient (3). Write it over the last digit (5) of the partial dividend -- and write the remainder beside the next digit of the dividend. Continue the operation, until there are no more digits in the dividend. |
|
Speak![]()
![]()
"7 goes into 25 three (3) times (21) with 4 left over."
Write the remainder 4 beside the 2. Continue:
"7 goes into 42 six (6) times exactly."
Compare the simplicity of that with long division:
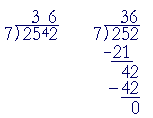
In long division, we bring down the 2 and write it next to the remainder 4. In short division, we simply write the remainder next to 2. Long division, moreover, de-emphasizes the spoken nature of arithmetic. It gives the false impression that, like algebra, arithmetic is a written skill.
Long division now properly belongs to the history of mathematics.
For no other reason than tradition, long division is still taught. Since both long and short division are nothing but methods, neither one requires a true understanding of division. That comes only with decomposing the dividend -- which in any case is the principle on which all methods are based.
Begin, "5 goes into 17 three (3) times (15) with 2 left over."
![]()
Write 3 over the 7 (not over the 1), and write the remainder 2 next to the 9.
Continue: "5 goes into 29 five (5) times (25) with 4 left over.
![]()
Write 5 over the 9, and write the remainder 4 next to the 8.
Finally, "5 goes into 48 nine (9) times (45) with 3 left over."
![]()
Write 9 over the 8. The final remainder is 3.
![]()
This problem will illustrate the following point:
| Upon placing the first digit in the quotient, then, over every digit in the dividend we must write a digit in the quotient. We proceed one digit at a time. |
![]()
We will write a digit over the 1, then over the 6, then over the 0, and so on, until finally we write a digit over the 3.
Begin,
"4 goes into 21 five (5) times (20) with remainder 1 ."
![]()
Next, "4 goes into 16 four (4) times exactly."
![]()
Next, "4 goes into 0 zero (0)."
![]()
Whenever the partial dividend is less than the divisor
-- 0 is less than 4 -- write 0 in the quotient.
Next, we must write a digit over the 2: "4 goes into 2 zero (0)."
![]()
Now the 2 remains. It is the remainder.
Whenever the quotient is 0, that digit beneath it
in the dividend is the remainder.
"4 goes into 24 six (6) times exactly."
![]()
Finally, "4 goes into 3 zero (0)."
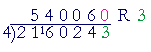
3 is the final remainder.
Again, whenever the quotient is 0, the digit beneath it in the dividend is the remainder.
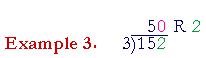
"3 goes into 15 five (5) times. 3 goes into 2 zero (0)."
2 is the remainder.
That is, 152 = 50 × 3 + 2.
We use short division whenever it is easy to multiply the divisor.
Example 4. Harold has a debt of $3,164. He is able to pay $25 a week. How many weeks will it take him to pay the debt?
Solution. How many 25's will equal 3,164. To find out, we must divide:
![]()
"25 goes into 31 one (1) time (25) with 6 left over."
![]()
"25 goes into 66 two (2) times (50) with 16 left over."
![]()
"25 goes into 164 six (6) times (150) with 14 left over."
![]()
At the end of 126 weeks, then, the debt will be almost paid. $14 will remain. Therefore, it will take Harold 127 weeks.
Problem. The multiples of 8 that are less than 100, are what percent of all the numbers less than 100?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
The multiples of 8 are the numbers 8, 16, 24, 32, and so on. How many multiples of 8 are contained in 100 -- that is, what number is 100 ÷ 8?
100 ÷ 8 = 12 R 4. That means, there are 12 eights less than 100. (12 × 8 = 96.) So the question is: 12 is what percent of 100?
The student should know immediately that the answer is 12% -- because that should be the first lesson in percent!
*
We will now consider the case in which the dividend is a decimal.
The divisor, we have seen (Lesson 11), must always be a whole number. (In Lesson 13 we will consider the case in which the divisor is a decimal.)
| 3. | How do we proceed when the dividend is a decimal? |
|
|
|
| Divide in the usual way. But on coming to the decimal point, place a decimal point above it in the quotient, and continue the operation. | |
"9 goes into 27 three (3) times."
"9 goes into 3 zero (0)."
Place the point in the quotient. The 3 remains.
"9 goes into 36 four (4) times.
To be clear about the meaning of a decimal quotient, see Example 12 in Section 2.
Solution. The divisor 7 is a whole number. Place the point:
![]()
When we have placed the point, then over each digit in the dividend we must write a digit in the quotient.
![]()
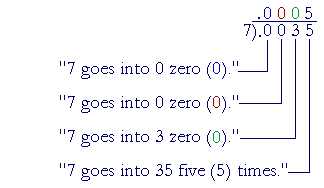
| * | * | * |
For those students still required to do problems in which the divisor has two or more digits, we include the following example. Note, however, that it can be done with short division.
Example 7. ![]()
38 will not go into 1; and it will not go into 17; but it will go into 174. The question is, How many times? To answer,
Try the first digit of the divisor, 3, into the first two digits of the dividend, 17.
![]()
3 goes into 17 five times. Therefore we do not have to try any number greater than 5. (Because any number greater than 5 × 38 will be too big. 5 × 30 = 150, which is less than 174, but 6 × 30 = 180; too big.)
5, in fact, is too big: 5 × 38 = 150 + 40 = 190.
(The student should try to do these simple multiplications mentally. It is the most efficient way to test a digit for the quotient.)
38 will go into 174 four (4) times:
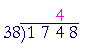
4 × 38 = 120 + 32 = 152.
To find the remainder -- what must we add to 52 to get 74?
52 + 22 = 74.
22 is the remainder.
![]()
In long division, we bring down the 8 and write it next to the remainder. In short division, we write the remainder next to 8.
How many times does 38 go into 228?
Again, try the first digit of the divisor, 3, into the first two digits of the dividend, 22. Although 3 goes into 22 seven (7) times, 7 is too big:
7 × 38 = 210 + 56 = 266.
38 will go in 6 times -- exactly:
![]()
6 × 38 = 180 + 48 = 228.
Note that we write the 4 in the quotient over the 4 in the dividend because we are putting 38 into 174.
We can then see immediately that the answer will have exactly two digits.
This problem may also be done by the traditional method of long division:
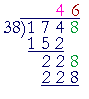
4 times 38 is 152. The remainder is 22. Bring down the 8.
38 goes into 228 six (6) times exactly.
All methods of division, including this one, are based on decomposing the dividend. For example,

We say, "4 goes into 35 eight (8) times with remainder 3."
But 5 -- and therefore 8 -- is in the tens place, so we are actually mutiplying 80 × 4 = 320, and 9 × 4 = 36:

The method itself decomposes 356 into multiples of 4: 320 + 36.
At this point, please "turn" the page and do some Problems.
or
Continue on to Section 2: Expressing the quotient as a decimal.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com

