Lesson 20 Section 2
Comparing fractions
| 10. | What is the relative size of fractions that have equal numerators? |
|
|
|
| The larger the denominator, the smaller the fraction. | |
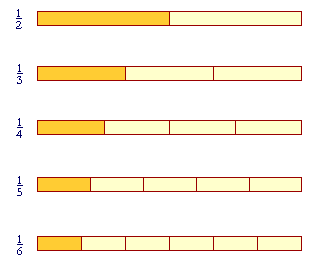
Those fractions are getting smaller. As the denominator -- the number of equal parts -- gets larger, then the size of each part gets
| smaller. | 1 6 |
is smaller than | 1 5 |
. |
Also, since one-sixth is smaller than one-fifth, then two will be smaller than two:
| 2 6 |
is smaller than | 2 5 |
. |
Three will be smaller than three:
| 3 6 |
is smaller than | 3 5 |
. |
And so on.
When frations have equal numerators, then the larger the denominator,
the smaller the fraction.
| 2 3 |
, | 2 4 |
, | 2 5 |
, | 2 6 |
. |
Those fractions are getting smaller.
In terms of ratios, the ratio of 1 to 2, for example, is greater than the ratio of 1 to 3:
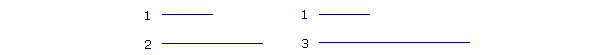
When we compare 1 with 2, it appears greater than when we compare it with 3.
| 11. | What is the relative size of fractions that have equal denominators? |
|
|
|
| The larger the numerator, the larger the fraction. | |
In this sequence,
| 2 6 |
, | 3 6 |
, | 4 6 |
, | 5 6 |
, |
the fractions are getting larger. Each one is one more of the 6 equal parts into which number 1 has been divided.
As for ratios, we say that the ratio of 2 to 5 is smaller than the ratio of 3 to 5:
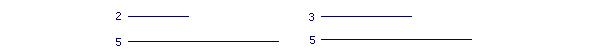
2, when compared with 5, appears smaller than 3 when compared with 5.
Example 1. Arrange these from smallest to largest:
| 5 7 |
4 9 |
4 7 |
| Solution. We must compare them in pairs. | 4 9 |
and | 4 7 |
have the same |
numerator; therefore
| 4 9 |
is smaller than | 4 7 |
. |
| 5 7 |
and | 4 7 |
have the same denominator; therefore |
| 5 7 |
is larger than | 4 7 |
. |
The sequence is
| 4 9 |
4 7 |
5 7 |
. |
| Example 2. Which is smaller, | 1 10 |
or | 2 9 |
? |
| Answer. Since | 1 10 |
is smaller than | 1 9 |
, then it is surely smaller than | 2 9 |
. |
In Lesson 23 we will see how to compare fractions with different numerators and denominators.
Please "turn" the page and do some Problems.
or
Continue on to the Section 3.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
