|
Lesson 4 Section 3 Scientific Notation
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
When is a number written in "scientific notation"?
How do we convert units in the metric system?
| 10. | When is a number written in "scientific notation"? |
| A number is written in scientific notation when there is one non-zero digit to the left of the decimal point. | |
2.345
That number is written in scientific notation. There is one digit to the left of the decimal point -- 2 -- and it is not 0.
In general, a number written in scientific notation will be multiplied by 10 raised to an "exponent."
2.345 × 103 2.345 × 10−3
Without going into the details of what the exponents 3 and −3 actually mean, we can state the following :
A positive exponent means to multiply by a power of 10. A negative exponent means to divide.
Briefly, the exponent indicates the number of 0's
in the power of 10. To go further into the meaning of an exponent, see Lessons 13 and 21 of Skill in Algebra.
Therefore, if a number is written in scientific notation, then to express it as a standard number, we can state the following rule:
If the exponent is positive, move the decimal point right as many places as indicated by the exponent.
If the exponent is negative, move the decimal point left as many places as indicated by the exponent.
Example 1. Each number is written in scientific notation. What standard number is it?
a) 5.42 × 103 = 5,420. Move the decimal point three places right.
b) 5.42 × 10−3 = .00542 Move the decimal point three places left.
Example 2. Write each number in scientific notation.
| a) | 123.4 = 1.234 × 10² |
| The scientific notation on the right begins 1.234. To get back to 123.4, we have to move the point 2 places right. We have to multiply by 10 with exponent +2. | |
An alternative explanation is based on the following:
A number does not change if we divide it and then multiply the quotient by the same number, or if we multiply and then divide by the same number.
And so to go from 123.4 to 1.234 we divided by 100. Therefore, for the original value not to change -- for the equal sign to mean equals -- we must multiply by 100, which is 10².
123.4 = 1.234 × 10²
We both divided and multiplied by 100.
| b) | 380,000 = 3.8 × 105 |
| The scientific notation on the right begins 3.8. To get back to 380,000, we have to move the point 5 places right. We have to multiply by 10 with exponent +5. | |
| Note that the 0's on 3.80000 would have been trailing 0's. We do not write them. | |
| Equivalently, beginning with 380,000, we divided by 100,000. To compensate, we then multiplied by 100,000 , which is 105. |
|
| c) | .0012 = 1.2 × 10−3 |
| The scientific notation begins 1.2. To get back to .0012, we have to move the point 3 places left. We have to multiply by 10 with exponent −3. | |
| Equivalently, we multiplied .0012 by 1000 and then divided by 1000 -- that is, we "multiplied" by 10−3. | |
Problem 1. Each of these is written in scientific notation. What standard number is it?
| a) | 2.401 × 103 = 2,401 | b) | 1.006 × 10² = 100.6 | ||
| c) | 7.01 × 105 = 701,000 | d) | 3.248 × 10 = 32.48 | ||
| e) | 1.86 × 10−4 = 0.000186 | f) | 4.05 × 10−1 = 0.405 | ||
| g) | 6.0 × 10−6 = 0.000006 | h) | 3.1 × 10−2 = 0.031 | ||
Problem 2. Write each of the following in scientific notation.
| a) | 1,234 = 1.234 × 103 | b) | 12.34 = 1.234 × 10 | |
| c) | 123.4 = 1.234 × 102 | d) | 2,400,000 = 2.4 × 106 | |
| e) | 0.000081 = 8.1 × 10−5 | f) | 0.00395 = 3.95 × 10−3 | |
| g) | 0.00000000628 = 6.28 × 10−9 | h) | 0.107 = 1.07 × 10−1 | |
The metric system
| 11. | What is the metric system? |
| It is the system of measurement based on the powers of 10 and their reciprocals. | |
| The metric unit of length is the meter, whose symbol is m. | |
| The metric unit of weight is the gram, whose symbol is gm. | |
| The metric unit of volume is the liter, whose symbol is L. | |
Here are metric prefixes that are in common use:
| Prefix | Symbol | Factor |
|---|---|---|
| tera | T | 1012 = 1,000,000,000,000 |
| giga | G | 109 = 1,000,000,000 |
| mega | M | 106 = 1,000,000 |
| kilo | k | 103 = 1,000 |
| centi | c |  |
| milli | m |  |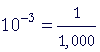
| micro | µ |  |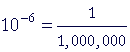
| nano | n |  |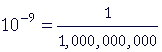
| pico | p |  |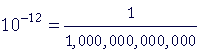
Thus km means kilometers, which is 103 or 1000 meters.
µgm mean micrograms, which is one-millionth of a gram.
| 12. | How do we convert units in the metric system? |
| 125 cm = ? m | |
| Use this Table and apply the rule given below. | |
| WHOLE UNITS | DECIMAL UNITS | |||||
|---|---|---|---|---|---|---|
| 4th order | 3rd order | 2nd order | 1st order | 1st order | 2nd order | 3rd order |
| 1000 | 100 | 10 | 1 | .1 | .01 | .001 |
| kilometer km | (hecto) | (deka) | meter m | (deci) | centimeter cm | millimeter mm |
| kilogram kg | gram gm | centigram cg | milligram mg | |||
| kiloliter kL | liter L | deciliter dL | centiliter cL | milliliter mL | ||
The 1st order or principle unit of length is the meter. The 2nd order unit (which is not in common use) is 10 times more and would have the prefix deka: 1 dekameter. The 3rd order unit (again not in common use) would have the prefix hecto, meaning 100 times. And the 4th order unit of length is the kilometer, which means 1000 meters.
As for the decimal units, the 1st order decimal unit is one-tenth of a meter, and is a called a decimeter ("dessi-meter") -- the prefix deci signifies the tenth part; but that measure of length is not in common use. The prefix centi signifies the hundredth part. The prefix milli signifies the thousandth part.
Relations between units of the same kind
The rule for expressing meters as kilometers, for example, or grams as centigrams, is as follows:
To convert to a different metric unit of the same kind, shift the decimal point
the same number of places, and in the same direction, left or right,
as the distance between the orders.
Example 1. 4235 m = ? km
Solution. Kilometers lie three orders to the left of meters. Therefore, simply separate three decimal digits in that same direction, from right to left:
4235 m = 4.235 km.
(Effectively, we have divided by 1000, for 1 kilometer is 1000 times 1 meter.)
Example 2. 5.2 gm = ? cg
Solution. Centigrams lie two orders to the right of grams. Therefore, shift the decimal point two places right.
5.2 gm = 520 cg
(Effectively, we have multiplied by 100, for 1 gram is 100 times 1 centigram.)
Example 3. 478 dL = ? kL
Solution. Kiloliters are four orders to the left of deciliters. Therefore, separate four decimal digits.
478 dL = .0478 kL
Problem 3.
a) If you change the whole number unit of 1st order to the unit of 4th a) order, how will you shift the decimal point?
Three places left.
b) Change each of the following to kilometers.
| 3285 m = 3.285 km | 296 m = .296 km | |
| 85 m = .085 km | 6.25 m = .00625 km | |
Problem 4.
a) If you change the whole number unit of 1st order to the decimal unit
a) of 2nd order, how will you shift the decimal point?
Two places right.
b) Change each of the following to centimeters.
| 1.658 m = 165.8 cm | 2.36 m = 236 cm | |
| 3.8 m = 380 cm | 15 m = 1500 cm | |
Problem 5. Convert the following.
| a) | 586 cm = 5.86 m | b) | 4.28 m = 4280 mm | |
| c) | 38.9 mL = 3.89 cL | d) | 1375 L = 1.375 kL | |
| e) | 12 gm = 1200 cg | f) | 1396 mg = .001396 kg | |
| g) | 6 km = 6000 m | h) | 6 km = 600,000 cm | |
| i) | 123 cg = 1.23 gm | j) | 123 cg = 1230 mg | |
| k) | 18 mL = .018 L | l) | 6.5 kL = 65,000 dL | |
Continue on to the next Lesson.
Introduction | Home | Table of Contents
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2012 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com