Lesson 27 Section 2
Parts of Fractions
Example 1 . A recipe calls for 6![]() cups of flour, and you are going to make a third of the recipe. How much flour will you use?
cups of flour, and you are going to make a third of the recipe. How much flour will you use?
Answer. A third of 6 cups is 2 cups. But how much is a third of ![]() ?
?
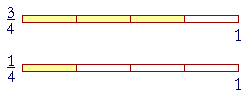
A third of ![]() is
is ![]() . Simply take a third of the numerator.
. Simply take a third of the numerator.
A third of 6![]() cups is 2
cups is 2![]() cups.
cups.
But say that the recipe calls for 6![]() cups of
flour. Since the numerator 1 does not have a third part, how will you take a third of
cups of
flour. Since the numerator 1 does not have a third part, how will you take a third of ![]() ?
?
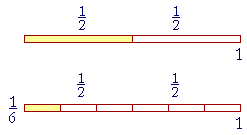
If we divide each ![]() into thirds, then the whole 1 will be in three times as many parts. A third of
into thirds, then the whole 1 will be in three times as many parts. A third of ![]() is
is ![]() .
.
To take a third of a fraction, simply multiply the denominator by 3.
A third of 6![]() cups is 2
cups is 2![]() cups.
cups.
There are two ways, then, to take a part of a fraction.
| 4. | How can we take a part of a fraction? |
| Take that part of the numerator -- if the numerator has that part. | |
| If the numerator does not have that part, | |
| multiply the denominator by the cardinal number that corresponds to the part. That is, to take half, multiply the denominator by 2; to take a third, multiply by 3; and so on. | |
Example 2.
| Half of | 6 7 |
is | 3 7 |
. | Take half of the numerator. | |
| A third of | 6 7 |
is | 2 7 |
. | Take a third of the numerator. | |
| A third of | 4 7 |
is | 4 21 |
. | 4 does not have a third part. Therefore multiply the denominator by 3. | |
| Example 3. How much is a fifth of | 1 2 |
? |
| Answer. | 1 10 |
. Multiply 2 by 5. |
| Example 4. How much is half of | 1 10 |
? |
| Answer. | 1 20 |
. Multiply 10 by 2. |
| Example 5. | 1 8 |
is which part of | 1 2 |
? |
| Answer. Since 8 is 4 × 2, | 1 8 |
is the fourth part, or one quarter, of | 1 2 |
. |
| Example 6. | 1 16 |
is which part of | 1 8 |
? What ratio has | 1 32 |
to | 1 8 |
? |
| Answer. | 1 16 |
is half of | 1 8 |
. 16 = 2 × 8. | 1 32 |
is a fourth of | 1 8 |
. 32 = 4 × 8. |
| Example 7. Percent. Since | 1 8 |
is half of | 1 4 |
(8 = 2 × 4), |
| and since | 1 4 |
is equal to 25%, then what percent is | 1 8 |
? |
Answer. Half of 25%, which is 12½%. (Lesson 16, Example 4.)
Now, each eighth will be another 12½%.
| 2 8 |
= | 1 4 |
= 12½% + 12½% = 25%. |
| 3 8 |
= | 25% + 12½% = 37½%. |
| 4 8 |
= | 1 2 |
= 50%. |
| 5 8 |
= | 50% + 12½% = 62½%. |
| 6 8 |
= | 3 4 |
= 75%. |
| 7 8 |
= | 75% + 12½% = 87½%. |
See Problem 15.
| Example 8. | 2 5 |
is larger than | 2 25 |
. (Lesson 23, Question 1.) How many |
times larger?
Answer. Five times larger. Because 25 is 5 × 5.
Example 9. The following problem appeared in a recent textbook:
| 1 5 |
is | 1 2 |
of what number? |
The writer no doubt intend it to be translated as
| 1 2 |
times what number is | 1 5 |
? |
-- thus making it a division problem:
| 1 5 |
÷ | 1 2 |
. |
However, if we make verbal sense of the problem --
1-fifth is half of what number?
-- then the answer is obvious. Just as 1 apple is half of 2 apples, so
1-fifth is half of 2-fifths.
| Example 10. | 3 7 |
is half of what number? |
| Answer. | 3 7 |
is half of | 6 7 |
. |
| Example 11. | 3 7 |
is a third of what number? |
| Answer. | 3 7 |
is a third of | 9 7 |
, which is 1 | 2 7 |
. |
Example 12. To make an orange dye, 3 parts of red dye are mixed with 2 parts of yellow dye. To make a green dye, 2 parts of blue dye are mixed with 1 part of yellow dye. If equal amounts of orange and green are mixed, what fraction of the new mixture is yellow dye?
Solution. For convenience, let
O = Orange dye, R = Red dye, Y = Yellow dye,
G = Green dye, B = Blue dye.
Now, the orange dye consists of a total of five parts: 3 parts red and 2 parts yellow. That is,
| O | = | 3 5 |
R + | 2 5 |
Y. |
The green dye consists of three parts: 2 parts blue and 1 part yellow.
| G | = | 2 3 |
B + | 1 3 |
Y. |
To add equal amounts of O and G, we may simply add half of each. Therefore, half of O is
| O | = | 3 10 |
R + | 1 5 |
Y. |
And half of G is
| O | = | 1 3 |
B + | 1 6 |
Y. |
Upon adding those equal parts of O and G, the new mixture will consist of
| 3 10 |
R + | 1 5 |
Y + | 1 3 |
B + | 1 6 |
Y. |
The LCM of those fractions is 30. (Lesson 23.) The fractions of Y --
| 1 5 |
Y + | 1 6 |
Y | ||
| -- become | |||||
| 6 30 |
Y + | 5 30 |
Y = | 11 30 |
Y. |
| 11 30 |
is the fraction of yellow dye in the new mixture. |
*
| Consider "Half of | 5 8 |
" -- which we know is | 5 16 |
-- and let us write it in |
symbols as
| 1 2 |
× | 5 8 |
. |
We now see why we multiply the numerators and multiply the denominators:
| 1 2 |
× | 5 8 |
= | 5 16 |
. |
It follows, as it must, from what the symbols mean.
| Similarly, Half of | 6 8 |
becomes |
| 1 2 |
× | 6 8 |
= | 3 8 |
. |
"2 goes into 6 three (3) times."
| Example 13. How much is a third of | 5 7 |
? How much is two thirds? |
| Answer. | A third of | 5 7 |
is | 5 21. |
(Multiply the denominator by 3). |
| Two thirds of | 5 7 |
is twice as much as one third: 2 × | 5 21 |
= | 10 21 |
. |
In symbols,
| 2 3 |
× | 5 7 |
= | 10 21 |
. |
| "Two thirds of | 5 7 |
is | 10 21 |
." |
And so we have arrived where we began (Lesson 26, Question 3), at the formal rule for multiplying fractions:
Multiply the numerators and multiply the denominators.
Please "turn" the page and do some Problems.
or
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
