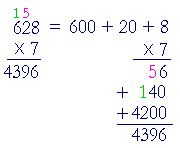Lesson 10
HOW TO MULTIPLY WHOLE NUMBERS
HOW TO MULTIPLY DECIMALS
In this Lesson, we will answer the following:
Multiplication by a whole number is repeated addition of the number being multiplied.
7 × 628
| 1. | How do we multiply by a single digit? |
| Align the multiplier (on the bottom) with the ones digit of the multiplicand (on top), and draw a line. Then multiply each digit of the multiplicand. Write the ones digit of each product below the line. If there is a tens digit, carry it -- add it -- to the next product. |
|
"7 times 8 is 56." Write 6, carry 5.
"7 times 2 is 14, plus 5 is 19." Write 9, carry 1.
"7 times 6 is 42, plus 1 is 43." Write 43.
That is,
7 × 628 = 4396.
Why can we repeatedly add 628 in that way? Because we have distributed 7 to the Tens, Ones, Hundreds of 628, and then added those partial products:
When the multiplier has more than one digit --
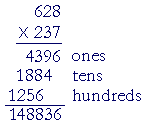
-- follow the same procedure for each digit. When we multiply by 3 tens, the product is 1884 tens. It is not necessary to write 18840. (Lesson 2.) Simply begin the 4 of 1884 in the tens column.
When we multiply by 2 hundreds, the product is 1256 hundreds, and so we write 6 in the hundreds column.
We can state the rule as follows:
| 2. | In writing, how do we multiply whole numbers? | ||
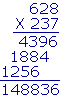 |
|||
| Write the multiplier under the multiplicand and draw a line. Multiply the multiplicand by each digit of the multiplier. Place the ones digit of each partial product in the same column as the multiplying digit. Then add the partial products. | |||
Anticipating the next Question, if there were decimal points --
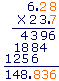
-- the multiplication would proceed in exactly the same way. In the answer, we would then separate as many decimal digits as there are in the two numbers together; in this case, three.
| Example 1. | 96 | |
| × 37 | ||
| 672 | ← 7 × 96 = 630 + 42 | |
| 2884 | ← 3 × 96 = 270 + 18 | |
| 3552 |
On multiplying by 7 ones, write 2 in the ones column.
On multiplying by 3 tens, write 8 in the tens column -- because the partial product 288 means 288 tens.
The student should be able to calculate each partial product mentally by distributing from left to right. We have indicated that above.
Example 2. Multiply 45 × 236.
It does not matter which number you choose as the multiplier, that is, to place on the bottom. However it is more efficient to choose 45 because then there will be only two multiplications rather than three.
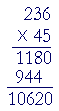
Example 3. 0's within the multiplier.
| 907 |
| × 308 |
| 7256 |
| 272156 |
| 279356 |
| 8 × 907 | = | 7200 + 56 | = | 7256 |
| 0 × 907 | = | 0 | ||
| 3 × 907 | = | 2700 + 21 | = | 272150 |
On multiplying by 8 ones, write 6 in the ones column.
Any number times 0 is 0, therefore it is not necessary to write anything in the tens column.
On multiplying by 3 hundreds, write 1 in the hundreds column.
It is not necessary to write rows of 0's. They add nothing to the product.
We are now about to see that we can do arithmetic only with whole numbers -- and then correctly place the decimal point.
| 3. | How do we multiply decimals? |
| .2 × 6.03 | |
|
Ignore the decimal points -- do not align them -- and multiply the numbers as whole numbers. Then, starting from the right of the product, separate as many decimal digits as there are in the two numbers together. |
|
Example 4. .2 × 6.03
Solution. Ignore the decimal points. Simply multiply
2 × 603 = 1206
Now we must place the decimal point. Together, .2 and 6.03 have three decimal digits. (Lesson 4, Problem 11.) Therefore, starting from the right, separate three digits:
1.206
When we ignore a decimal point, we have in effect moved the point to the right:
6.03 → 603
We have multiplied by a power of 10. (Lesson 4, Question 2.) To name the right answer, then, we
must divide by that power: we must separate
the same number of decimal digits. For, a number
does not change if we multiply it and then divide
by the same number. (Lesson 11.)
Example 5. .04 × .011
Solution. When we ignore the decimal points --
04 × 011
-- then those are leading 0's. They add nothing to the value. Simply multiply
4 × 11 = 44.
Now, .04 and .011 together have five decimal digits. Therefore the product will have five decimal digits -- it will look like this:
._ _ _ _ _
Here is the product:
.0 0 0 4 4
Example 6. 200 × .012
Solution. Ignore the decimal point. Multiply
200 × 12 = 2400
Again, to multiply whole numbers that end in 0's, first ignore the 0's, then replace them. (Lesson 9, Question 2.) But replace only the 0's on the end of whole numbers. Do not replace the 0 of .012
Now separate three decimal digits (.012):
2.400 = 2.4
| 4. | How can we find a percent of a whole number? |
| 6% of $45 | |
| Multiply the percent times the number, then separate two decimal digits. | |
6 × 45 = 6 × 40 + 6 × 5 = 240 + 30 = 270.
On separating two decimal digits:
6% of $45 is $2.70.
That, in any event, is what we would do if we changed 6% to .06 (Lesson 4), and multiplied .06 × 45.
Equivalently, since
1% of $45 is $.45
(Lesson 4), then 6% will be 6 times 1%, that is, 6 × .45.
Note: Because of the order property of multiplication,
| 6% of $45 | = | 45% of $6. |
| .06 × 45 | = | .45 × 6. |
As another example, since 50% means half:
24% of 50 = 50% of 24 = 12.
Example 7. How much is 9% of $84?
Solution. Multiply 9 × 84, then separate two decimal digits.
On distributing 9 to 80 + 4:
9 × 84 = 720 + 36 = 756.
9% of $84 is $7.56.
Example 8. How much is 3% of $247?
Solution. 3 × 247 = 600 + 120 + 21 = 741.
3% of $247 is $7.41.
Example 9. How much is 11% of $76?
Solution. 11 × 76 = 760 + 76 = 836. (Lesson 9.)
11% of $76 is $8.36.
These are simple problems that do not require a calculator. For more such simple problems, see Lesson 29. To learn how to do percent problems with a calculator, see Lesson 14.
What is "1 square foot"?
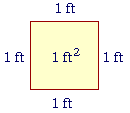
1 square foot is a square figure in which each side is 1 foot.
We abbreviate "1 square foot" as 1 ft².
1 foot (1 ft) is a unit to measure length. When it is the unit of length, then 1 square foot (1 ft²) is the unit of area. And similarly for any unit of length and the corresponding unit of area.
Now here is a rectangle whose base is 3 cm and whose height is 2 cm.
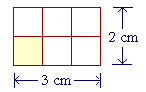
What do we call the small shaded square?
Since each side is 1 cm, we call it "1 square centimeter." And we can see that the entire figure is made up 2 × 3 or 6 of them.
In other words, the area of that rectangle -- the space enclosed by the boundary -- is 6 square centimeters: 6 cm².
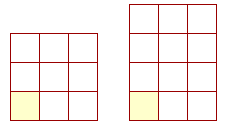
If the rectangle were 3 by 3 -- that is, if it were a square -- then it would be made up of 9 cm². If it were 3 by 4, the area would be 12 cm². And so on. In every case, to calculate the area of a rectangle, simply multiply the base times the height.
Area = Base × Height
When the length is measured in centimeters, the area is measured in square centimeters: cm². And similarly for any unit of length.
You sometimes see
3 cm × 4 cm = 12 cm²,
which to be honest make no sense. The multiplier (on the left) shows the number of times to repeatedly add the multiplicand (on the right). Therefore the multiplier must always be a pure number.
3 × 4 cm² = 12 cm².
We have illustrated this with whole numbers, but it will be true for any numbers.
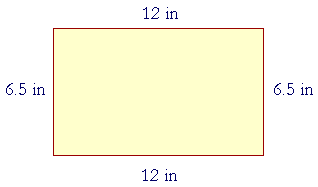
If the base is 12 in, and the height is 6.5 in, then to find the area, multiply
12 × 6.5
Now,
12 × 65 = 10 × 65 + 2 × 65 = 650 + 130 = 780.
Therefore on separating one decimal digit (6.5):
Area = 78 in².
Problem 1. 1 yd = 3 ft. 1 square yard is composed of now many square feet?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
9 square feet.
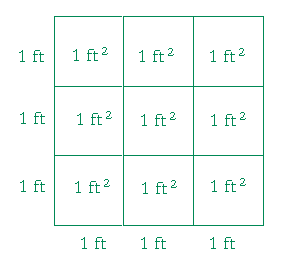
Problem 2. The price of a carpet is $50 a square yard. What is the approximate price of a carpet that is 5 ft by 7 ft?
Approximately $200.
The area of the 5 by 7 carpet is 35 square feet. A square yard is 9 square feet. That carpet is approximatly 4 square yards. Therefore the price is approximately 4 times $50, which is $200.
Please "turn" the page and do some Problems.
or
Continue on to the Next Lesson.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com