S k i l l
 i n
A R I T H M E T I C

Table of Contents | Home | Introduction

RATIO AND PROPORTION  1

Lesson 16  Section 3



 4.   How can we express the ratio of any smaller number to a larger?
2 to 3
 
  Let each number say its name. Let the smaller number say its cardinal name: One, two, three,.... Let the larger number say its ordinal name: third, fourth, fifth,....

Example 1.   What ratio has 2 to 3?

Answer.  "2 is two thirds of 3."

2 says its cardinal name, "Two."  3 says its ordinal name, "third."

That is how to express the ratio of any smaller number to a larger.

Example 2.   What ratio has 4 to 5?

Answer.  "4 is four fifths of 5."

To see this, consider that 1 is one fifth of 5:

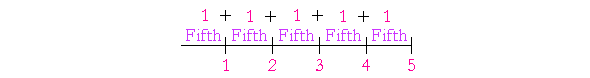
1 + 1 + 1 + 1 + 1

2 is two fifths of 5.

3 is three fifths of 5.

4 is four fifths of 5.

Each number says its name.

Lowest terms

The two numbers of a ratio are called its terms.  In the ratio of 4 to 12,
4 and 12 are the terms.
 5.   When is a ratio expressed with the lowest terms?
 
  When it is expressed with the smallest numbers which have that ratio.

Many pairs of numbers have the same ratio as 4 and 12, for example.
5 and 15,  6 and 18,  10 and 30.   And so on.  But the smallest pair are 1 and 3.

4 is to 12  as 1 is to 3.

Now, it is perfectly correct to say,

"4 is four twelfths of 12."

But when we say,

"4 is one third of 12,"

then we have expressed that ratio with the lowest terms, that is, with the smallest numbers which have that ratio.  The terms 1 and 3 say their names.
 6.   How can we know when the ratio of two numbers is expressed with the lowest terms?
 
  1 is their only common divisor.

Example 3.   The ratio of 7 to 8 expressed as seven eighths is with the lowest terms, because 1 is the only common divisor of 7 and 8.  But the ratio of 12 to 18 expressed as twelve eighteenths, although true, is not with the lowest terms, because 12 and 18 have a common divisor 6.

 7.   What is the Theorem of the Common Divisor?
 
  "If two numbers are divided by the same number, then the quotients will have the same ratio as the numbers divided."

(In the next Lesson, we will see why.)

Example 4.   What ratio has 12 to 18?

Answer.  12 and 18 have a common divisor 6:

"6 goes into 12 two times and into 18 three times."

The quotients are 2 and 3.  Therefore according to the theorem,

12 is to 18  as  2 is to 3.

"12 is two thirds of 18."

2 and 3 say their names.

Example 5.   Express the ratio of 21 to 28 with the lowest terms.

Answer.  Their ratio will be expressed with a sentence,

"21 is               28."

21 and 28 have a common divisor 7:

"7 goes into 21 three times and into 28 four times."

21 is to 28  as  3 is to  4.

"21 is three fourths of 28."

21 is three fourths of 28.

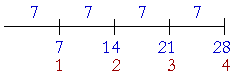
Notice that their common divisor, 7, is one fourth of 28.

Example 6.   If a is an eighth of b,  then  a is to b  as  ? is to ?.

Complete that proportion with the smallest numbers -- the lowest terms -- which have that ratio.

(a simply means the first term, and b, the second.)

Answer.  There are many pairs such that the first is an eighth of the second.  2 and 16;  5 and 40;  10 and 80.  However, the smallest such numbers are 1 and 8.

If a is an eighth of b,  then  a is to b  as  1 is to 8.


Application to percent

Example 7.   If a is 25% of b, then a is to b  as  ? is to ?.

Complete that proportion with the smallest numbers -- the lowest terms -- which have that ratio.

Answer.   Since 25% means a quarter, then

a is to b  as  1 is to 4.


Example 8.   In a class, the ratio of girls to boys is 3 to 4.

That means there are 3 girls in the class for every 4 boys.

If there are 24 boys, then how many girls are there?

Solution.  "The ratio of girls to boys is 3 to 4."  What ratio has 3 to 4? 3 is three fourths of 4. (Lesson 16.)  Therefore, the number of girls is three fourths of the number of boys -- three fourths of 24.  One fourth of 24 is 6. Therefore, three fourths are 18.

(See Lesson 14, Questions 4 and 5.  And for another solution to this problem, see Example 11 of the next Lesson.)

Note:  We could have worded this problem as follows:

"The girls are 75% of the boys."

That means that the girls are to the boys as 3 is to 4 -- because 75% is three fourths of 100%.  (Compare Example 7.)


Example 9.  The whole is equal to the sum of the parts.   In a class, the number of girls is 75% of the boys.  There are 35 students.  How many girls are there and how many boys?

Solution.   To say that girls are 75% of the boys, is to say that the ratio of

girls to boys is 3 to 4.  But that means that 3 out of every 7 students are girls (3 + 4 = 7), and 4 out of every 7 are boys. In other words, three sevenths of the students are girls, and four sevenths are boys.

Now, one seventh of 35 is 5.  Therefore three sevenths are 3 × 5 = 15.  There are 15 girls.  The rest, then -- 35 − 15 = 20 -- are boys.

(For for another solution to this problem, see Example 12 of the next Lesson.  For more on the locution "out of," see the next Lesson and Lesson 19.)

Example 10.   In a survey, the number of Yes's were 50% of the number of No's.  What percent of the entire survey responded Yes?

Solution.   To say that the Yes's were 50% of No's, is to say that the Yes's were to the No's in the ratio 1 to 2.

In other words, 1 out of every 3 responses -- one third -- were Yes.

They were 33 1
3		 % of the entire survey.  (Lesson 15, Question 6.)

Please "turn" the page and do some Problems.

or


Introduction | Home | Table of Contents

Please make a donation to keep TheMathPage online.
Even $1 will help.

Copyright © 2001-2008 Lawrence Spector

Questions or comments?

E-mail:  themathpage@nyc.rr.com