Lesson 37, Quadratic equations: Section 2
Proof of the quadratic formula
IN LESSON 18 we saw a technique called completing the square. We will now apply it to solving a quadratic equation.
Completing the square
If we try to solve this quadratic equation by factoring,
| x2 + 6x + 2 | = | 0 |
| we cannot. Therefore, we will employ a method called completing the square. We will make the quadratic take the form of a perfect square trinomial: | ||
| a2 + 2ab + b2 | = | (a + b)2 . |
This method is valid only when the coefficient of x2 is 1.
1) Transpose the constant term to the right
x2 + 6x = −2.
| 2) | Add a square number to both sides: Add the square of half the coefficient of x. In this case, add the square of 3: |
x2 + 6x + 9 = −2 + 9.
The left-hand side is now the perfect square of (x + 3).
(x + 3)2 = 7.
That has the form
| a2 | = | b | |
| which implies | |||
| a | = | ± |
|
| Therefore, | |||
| x + 3 | = | ± |
|
| x | = | −3 ± |
|
The solutions are the conjugate pair:
−3 + ![]() , −3 −
, −3 − ![]() .
.
For a method of checking those roots, see the theorem of the sum and product of the roots: Lesson 10 of Topics in Precalculus,
In Lesson 18 there are examples and problems in which the coefficient of x is odd. Also, some of the quadratics below have complex roots, and some involve simplifying radicals.
Problem 6. Solve each quadratic equation by completing the square.
To see the answer, pass your cursor from left to right
over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | x2 − 2x − 2 | = | 0 | b) | x2 − 10x + 20 | = | 0 | |
| x2 − 2x | = | 2 | x2 − 10x | = | −20 | |||
| x2 − 2x + 1 | = | 2 + 1 | x2 − 10x + 25 | = | −20 + 25 | |||
| (x − 1)2 | = | 3 | (x − 5)2 | = | 5 | |||
| x − 1 | = | ± |
x − 5 | = | ± |
|||
| x | = | 1 ± |
x | = | 5 ± |
|||
| c) | x2 − 4x + 13 | = | 0 | d) | x2 + 6x + 29 | = | 0 | |
| x2 − 4x | = | −13 | x2 + 6x | = | −29 | |||
| x2 − 4x + 4 | = | −13 + 4 | x2 + 6x + 9 | = | −29+ 9 | |||
| (x − 2)2 | = | −9 | (x + 3)2 | = | −20 | |||
| x − 2 | = | ±3i | x + 3 | = | ± |
|||
| x | = | 2 ± 3i | x | = | −3 ± 2i |
|||
| e) | x2 − 5x − 5 | = | 0 | f) | x2 + 3x + 1 | = | 0 | |
| x2 − 5x | = | 5 | x2 + 3x | = | −1 | |||
| x2 − 5x + 25/4 | = | 5 + 25/4 | x2 + 3x + 9/4 | = | −1 + 9/4 | |||
| (x − 5/2)2 | = | 5 + 25/4 | (x + 3/2)2 | = | − 1 + 9/4 | |||
| x − 5/2 | = | ± |
x + 3/2 | = | ± |
|||
| x | = | x | = | |||||
Problem 7. Find two numbers whose sum is 10 and whose product is 20.
x = 5 ± ![]()
According to the theorem of the sum and products of the roots, they are the solutions to Problem 6b above.
The quadratic formula
Here is a formula for finding the roots of any quadratic. It is proved by completing the square![]() In other words, the quadratic formula completes the square for us.
In other words, the quadratic formula completes the square for us.
Theorem. If
ax2 + bx + c = 0,
then
![]()
The two roots are on the right. One root has the plus sign; the other, the minus sign. If the square root term is irrational, then the two roots are a conjugate pair.
If we call those two roots r1 and r2 , then the quadratic can be factored as
(x − r1)(x − r2).
We will prove the quadratic formula below.
Example 4. Use the quadratic formula to solve this quadratic equation:
3x2 + 5x − 8 = 0
Solution. We have: a = 3, b = 5, c = −8.
Therefore, according to the formula:
| x | = | |
| = | ||
| = | ||
| = | ||
That is,
| x | = | −5 + 11 6 |
or | −5 − 11 6 |
| x | = | 6 6 |
or | −16 6 |
| x | = | 1 | or − | 8 3 |
. |
Those are the two roots. And they are rational. When the roots are rational, we could have solved the equation by factoring, which is always the simplest method.
| 3x2 + 5x − 8 | = | (3x + 8)(x − 1) | ||
| x | = | − | 8 3 |
or 1. |
Problem 8. Use the quadratic formula to find the roots of each quadratic.
a) x2 − 5x + 5
a = 1, b = −5, c = 5.
| x | = | = | = |
b) 2x2 − 8x + 5
a = 2, b = −8, c = 5.
| x | = | |||||||
| = | = | = | = | 2 ± ½ |
||||
c) 5x2 − 2x + 2
a = 5, b = −2, c = 2.
| x | = | |||||||
| = | = | = | 2 ± 6i 10 |
= | 1 ± 3i 5 |
|||
The discriminant
The radicand b2 − 4ac is called the discriminant. If the discriminant is
| A square number: | The roots are rational. |
| Positive but not a square number: | The roots are real and conjugate. |
| Negative: | The roots are complex and conjugate. |
| Zero: | The roots are rational and equal -- i.e. a double root. |
Problem 9. Show: If the roots of ax2 + bx + c are complex, and a, b, c are positive, then
2a − b + c > 0.
Since the roots are complex, then the discriminant b2 − 4ac < 0. That implies b2 < 4ac.
Now, 2a − b + c > 0 if and only if
b < 2a + c
if and only if
b2 < 4a2 + 4ac + c2,
which is true. For, since b2 < 4ac, it is less than 4ac plus a positive quantity. 4a2 and c2 are positive.
The student should be familiar with the logical expression
Proof of the quadratic formula
To prove the quadratic formula, we complete the square. But to do that, the coefficient of x2 must be 1. Therefore, we will divide both sides of the original equation by a:
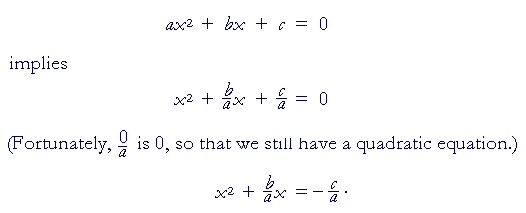
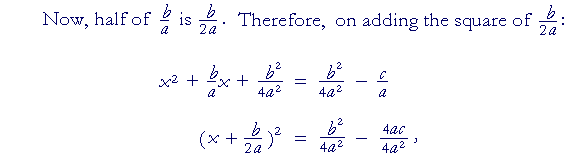
on multiplying both c and a by 4a, thus making the denominators the same (Lesson 23),
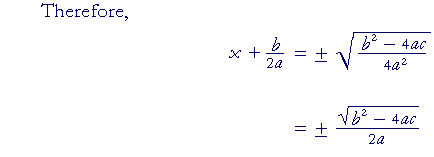
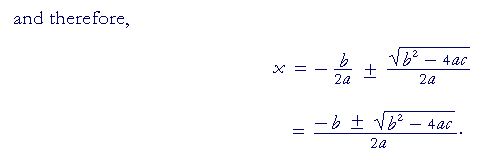
This is the quadratic formula.
Section 3: The graph of y = A quadratic
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com