19
THE DIFFERENCE
OF TWO SQUARES
Summary of Multiplying/Factoring
The sum and difference of odd powers
WHEN THE SUM of two numbers multiplies their difference --
(a + b)(a − b)
-- then the product is the difference of their squares:
(a + b)(a − b) = a2 − b2
For, the like terms will cancel. (Lesson 16.)
Symmetrically, the difference of two squares can be factored:
x2 − 25 = (x + 5)(x − 5)
x2 is the square of x. 25 is the square of 5.
The sum of two squares -- a2 + b2 -- cannot be factored. See Section 2.
Example 1. Multiply (x3 + 2)(x3 − 2).
Solution. Recognize the form:
(a + b)(a − b)
The product will be the difference of two squares:
(x3 + 2)(x3 − 2) = x6 − 4.
x6 is the square of x3. 4 is the square of 2.
Upon seeing the form (a + b)(a − b), the student should not do the FOIL method. The student should recognize immediately that the product will be a2 − b2.
That is skill in algebra.
And the order of factors never matters:
(a + b)(a − b) = (a − b)(a + b) = a2 − b2.
Problem 1. Write only final product..
a) (x + 9)(x − 9) = x2 − 81
b) (y + z)(y − z) = y2 − z2
c) (6x − 1)(6x + 1) = 36x2 − 1
d) (3y + 7)(3y − 7) = 9y2 − 49
e) (x3 − 8)(x3 + 8) = x6 − 64
f) (xy + 10)(xy − 10) = x2y2 − 100
g) (xy2 − z3)(xy2 + z3) = x2y4 − z6
h) (xn + ym)(xn − ym) = x2n − y2m
Problem 2. Factor.
a) x2 − 100 = (x + 10)(x − 10)
b) y2 − 1 = (y + 1)(y − 1)
c) 1 − 4z2 = (1 + 2z)(1 − 2z)
d) 25m2 − 9n2 = (5m + 3n)(5m − 3n)
e) x6 − 36 = (x3 + 6)(x3 − 6)
f) y4 − 144 = (y2 + 12)(y2 − 12)
g) x8 − y10 = (x4 + y5)(x4 − y5)
h) x2n − 1 = (xn + 1)(xn − 1)
Problem 3. Factor completely.
| a) x4 − y4 | = | (x2 + y2)(x2 − y2) |
| = | (x2 + y2)(x + y)(x − y) | |
| b) 1 − z8 | = | (1 + z4)(1 − z4) |
| = | (1 + z4)(1 + z2)(1 − z2) | |
| = | (1 + z4)(1 + z2)(1 + z)(1 − z) | |
Problem 4. Completely factor each of the following. First remove a common factor. Then factor the difference of two squares.
a) xy2 − xz2 = x(y2 − z2) = x(y + z)(y − z)
b) 8x2 − 72 = 8(x2 − 9) = 8(x + 3)(x − 3)
c) 64z − z3 = z(64 − z2) = z(8 + z)(8 − z)
d) rs3 − r3s = rs(s2 − r2) = rs(s + r)(s − r)
e) 32m2n − 50n3 = 2n(16m2 − 25n2) = 2n(4m + 5n)(4m − 5n)
f) 5x4y5 − 5y5 =
f) 5y5(x4 − 1) = 5y5(x2 + 1)(x + 1)(x − 1)
Geometrical algebra
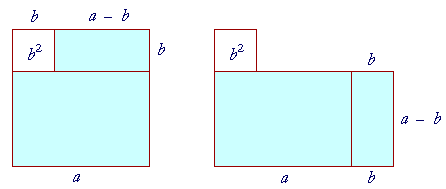
The entire figure on the left is a square on side a. The square b2 has been inserted in the upper left corner, so that the shaded area is the difference of the two squares, a2 − b2.
Now, in the figure on the right, we have moved the rectangle (a − b)b to the side. The shaded area is now equal to the rectangle
(a + b)(a − b).
That is,
a2 − b2 = (a + b)(a − b).
*
The Difference of Two Squares completes our study of products of binomials. Those products come up so often that the student should be able to recognize and apply each form.
Summary of Multiplying/Factoring
In summary, here are the four forms of Multiplying/Factoring that characterize algebra.
| 1. Common Factor | 2(a + b) | = | 2a + 2b | |
| 2. Quadratic Trinomial | (x + 2)(x + 3) | = | x2 + 5x + 6 | |
| 3. Perfect Square Trinomial | (x − 5)2 | = | x2 − 10x + 25 | |
| 4. The Difference of Two Squares | (x + 5)(x − 5) | = | x2 − 25 | |
Problem 5. Distinguish each form, and write only the final product.
a) (x − 3)2 = x2 − 6x + 9. Perfect square trinomial.
b) (x + 3)(x − 3) = x2 − 9. The difference of two squares.
c) (x − 3)(x + 5) = x2 + 2x − 15. Quadratic trinomial.
d) (2x − 5)(2x + 5) = 4x2 − 25. The difference of two squares.
e) (2x − 5)2 = 4x2 − 20x + 25. Perfect square trinomial.
f) (2x − 5)(2x + 1) = 4x2 − 8x − 5. Quadratic trinomial.
Problem 6. Factor. (What form is it? Is there a common factor? Is it the difference of two squares? And so on. )
a) 6x − 18 = 6(x − 3). Common factor.
b) x6 + x5 + x4 + x3 = x3(x3 + x2 + x + 1). Common factor.
c) x2 − 36 = (x + 6)(x − 6). The difference of two squares.
d) x2 − 12x + 36 = (x − 6)2. Perfect square trinomial.
e) x2 − 6x + 5 = (x − 5)(x − 1). Quadratic trinomial.
f) x2 − x − 12 = (x − 4)(x + 3)
g) 64x2 − 1 = (8x + 1)(8x − 1)
h) 5x2 − 7x − 6 = (5x + 3)(x − 2)
i) 4x5 + 20x4 + 24x3 = 4x3(x2 + 5x + 6) = 4x3(x + 3)(x + 2)
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
