Lesson 35
Simultaneous equations: Section 2
Cramer's Rule: The method of determinants
Example 4. Solve this system of simultaneous equations:
| 1) | 3x | + | 4y | = | 19 |
| 2) | 2x | − | y | = | 9 |
Solution. If we add the equations as they are, neither one of the unknowns will cancel. Now, if the coefficient of y in equation 2) were −4, then the y's would cancel. Therefore we will expand our strategy as follows:
Make one pair of coefficients negatives of one another -- by multiplying
both sides of an equation by the same number. Upon adding the equations, that unknown will be eliminated.
To make the coefficients of the y's 4 and −4, we will multiply both sides of equation 2) by 4 :
| 1) | 3x | + | 4y | = | 19 | 3x | + | 4y | = | 19 | |
| 2) | 2x | − | y | = | 9 | 8x | − | 4y | = | 36 | |
| 11x | = | 55 | |||||||||
| x | = | 55 11 |
|||||||||
| x | = | 5 | |||||||||
The 4 over the arrow in equation 2) signifies that both sides of that equation have been multiplied by 4. Equation 1) has not been changed.
To solve for y, substitute x = 5 in either one of the original equations. In equation 1):
| 3 · 5 + 4y | = | 19 |
| 4y | = | 19 − 15 |
| 4y | = | 4 |
| y | = | 1 |
The solution is (5, 1).
The student should always verify the solution by replacing x and y with (5, 1) in the original equations.
Example 5. Solve simultaneously:
| 1) | 3x | + | 2y | = | −2 |
| 2) | 2x | + | 5y | = | −5 |
Solution. We must make one pair of coefficients negatives of one another. In this example, we must decide which of the unknowns to eliminate, x or y. In either case, we will make the new coefficients the Lowest Common Multiple (LCM) of the original coefficients -- but with opposite signs.
Thus, if we eliminate x, then we will make the new coeffients 6 and −6. (The LCM of 3 and 2 is 6.) While if we eliminate y, we will make their new coefficients 10 and −10. (The LCM of 2 and 5 is 10.)
Let us choose to eliminate x:
| 1) | 3x | + | 2y | = | −2 | 6x | + | 4y | = | −4 | |
| 2) | 2x | + | 5y | = | −5 | −6x | − | 15y | = | 15 | |
| ________________________________________________________________________ | |||||||||||
| − | 11y | = | 11 | ||||||||
| y | = | −1. | |||||||||
Equation 1) has been multiplied by 2. Equation 2) has been multiplied by −3 -- because we want to make those coefficients 6 and −6, so that on adding, they will cancel.
To solve for x, we will substitute y = −1 in the original equation 1):
| 3x + 2(−1) | = | −2 |
| 3x − 2 | = | −2 |
| 3x | = | 0 |
| x | = | 0 |
The solution is (0, −1).
Problem 3. Solve simultaneously.
| 1) | 2x | + | 3y | = | 13 |
| 2) | 5x | − | y | = | 7 |
To make the y's cancel, multiply equation 2) by 3:
| 1) | 2x | + | 3y | = | 13 | 2x | + | 3y | = | 13 | |
| 2) | 5x | − | y | = | 7 | 15x | − | 3y | = | 21 | |
| ________________________________________________________________________ | |||||||||||
| 17x | = | 34 | |||||||||
| x | = | 2 | |||||||||
To solve for y:
Substitute x = 2 in one of the original equations.
In equation 1:
| 2 · 2 + 3y | = | 13 |
| 4 + 3y | = | 13 |
| 3y | = | 9 |
| y | = | 3 |
The solution is (2, 3).
Problem 4. Solve simultaneously.
| 1) | x | + | 2y | = | −1 |
| 2) | 2x | − | 3y | = | 5 |
To make the x's cancel, multiply equation 1) by −2:
| 1) | x | + | 2y | = | −1 | −2x | − | 4y | = | 2 | |
| 2) | 2x | − | 3y | = | 5 | 2x | − | 3y | = | 5 | |
| ________________________________________________________________________ | |||||||||||
| − | 7y | = | 7 | ||||||||
| y | = | −1 | |||||||||
To solve for x:
Substitute y = −1 in one of the original equations.
In equation 1:
| x + 2(−1) | = | −1 |
| x − 2 | = | −1 |
| x | = | −1 + 2 |
| x | = | 1 |
The solution is (1, −1).
We could have eliminated y by multiplying equation 1) by 3 and equation 2) by 2.
Problem 5. Solve simultaneously:
| 1) | 3x | − | 4y | = | 1 |
| 2) | 2x | + | 3y | = | 12 |
To make the y's cancel:
Multiply equation 1) by 3 and equation 2) by 4:
| 1) | 3x | − | 4y | = | 1 | 9x | − | 12y | = | 3 | |
| 2) | 2x | + | 3y | = | 12 | 8x | + | 12y | = | 48 | |
| ________________________________________________________________________ | |||||||||||
| 17x | = | 51 | |||||||||
| x | = | 51 17 |
|||||||||
| x | = | 3 | |||||||||
To solve for y:
Substitute x = 3 in one of the original equations.
In equation 2 (because the sign of y is already positive):
| 2 · 3 + 3y | = | 12 |
| 6 + 3y | = | 12 |
| 3y | = | 6 |
| y | = | 2 |
The solution is (3, 2).
Problem 6. Solve simultaneously:
| 1) | 3x | + | 2y | = | −4 |
| 2) | 2x | + | 5y | = | 1 |
To make the x's cancel:
Multiply equation 1) by 2 and equation 2) by −3:
| 1) | 3x | + | 2y | = | −4 | 6x | + | 4y | = | −8 | |
| 2) | 2x | + | 5y | = | 1 | −6x | − | 15y | = | −3 | |
| ________________________________________________________________________ | |||||||||||
| − | 11y | = | −11 | ||||||||
| y | = | 1 | |||||||||
To solve for x:
Substitute y = 1 in one of the original equations.
In equation 1:
| 3x + 2 · 1 | = | −4 |
| 3x + 2 | = | −4 |
| 3x | = | −4 − 2 |
| 3x | = | −6 |
| x | = | −2 |
The solution is (−2, 1).
We could have eliminated y by multiplying equation 1) by 5 and equation 2) by −2.
Problem 7. Solve simultaneously:
| 1) | 5x | + | 3y | = | −11 |
| 2) | 2x | + | 4y | = | −10 |
To make the x's cancel:
Multiply equation 1) by 2 and equation 2) by −5:
| 1) | 5x | + | 3y | = | −11 | 10x | + | 6y | = | −22 | |
| 2) | 2x | + | 4y | = | −10 | −10x | − | 20y | = | 50 | |
| ________________________________________________________________________ | |||||||||||
| − | 14y | = | 28 | ||||||||
| y | = | −2 | |||||||||
To solve for x:
Substitute y = −2 in one of the original equations.
In equation 1:
| 5x + 3(−2) | = | −11 |
| 5x − 6 | = | −11 |
| 5x | = | −11 + 6 |
| 5x | = | −5 |
| x | = | −1 |
The solution is (−1, −2).
We could have eliminated y by multiplying equation 1) by 4 and equation 2) by −3.
Cramer's Rule: The method of determinants
A system of two equations in two unknowns has this form:
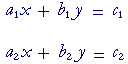
The a's are the coefficients of the x's. The b's are the coefficients of the y's. The following is the matrix of those coefficients.
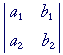
The number a1b2 − b1a2 is called the determinant of that matrix.
| det | 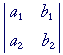 |
= | a1b2 − b1a2 |
Let us denote that determinant by D.
Now consider this matrix in which the c's replace the coefficients of the x's:
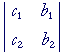
Then the determinant of that matrix -- which we will call Dx -- is
c1b2 − b1c2
And consider this matrix in which the c's replace the coeffients of the y's:
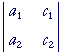
The determinant of that matrix -- Dy -- is
a1c2 − c1a2
Cramer's Rule then states the following:
In every system of two equations in two unknowns
in which the determinant D is not 0,
| x | = | Dx D |
| y | = | Dy D |
Example. Use Cramer's Rule to solve this system of equations (Problem 7):
| 5x | + | 3y | = | −11 |
| 2x | + | 4y | = | −10 |
Solution.
| D | = | det | = | 5 · 4 − 3 · 2 | |
| = | 20 − 6 | ||||
| = | 14. | ||||
| Dx | = | det | = | −11 · 4 − 3 · −10 | |
| = | −44 + 30 | ||||
| = | −14. | ||||
| Dy | = | det | = | 5 · −10 − (−11) · 2 | |
| = | −50 + 22 | ||||
| = | −28. | ||||
Therefore,
| x | = | Dx D |
= | −14 14 |
= | −1. |
| y | = | Dy D |
= | −28 14 |
= | −2. |
Problem. Use Cramer's Rule to solve these simultaneous equations.
| 3x | − | 5y | = | −31 |
| 2x | + | y | = | 1 |
| D | = | det | = | 3 · 1 − (−5) · 2 | |
| = | 3 + 10 | ||||
| = | 13. | ||||
| Dx | = | det | = | −31 · 1 − (−5) · 1 | |
| = | −31 + 5 | ||||
| = | −26. | ||||
| Dy | = | det | = | 3 · 1 − (−31) · 2 | |
| = | 3 + 62 | ||||
| = | 65. | ||||
Therefore,
| x | = | Dx D |
= | −26 13 |
= | −2. |
| y | = | Dy D |
= | 65 13 |
= | 5. |
When the determinant D is not 0, we say that the equations are linearly independent. In any system of linearly independent equations, there is one and only one solution.
When the determinant D is 0, then either 1) there is not a unique solution, it is possible to name many; or 2) there is no solution at all. In case 1), the equations are linearly dependent. One of them is simply a multiple of the other. For example,
x + y = 3
2x + 2y = 6.
In case 2), the equations are inconsistent.
x + y = 3
x + y = 4.
Section 3: Three equations in three unknowns
Next Lesson: Word problems that lead to simultaneous equations
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com