The slope of a straight line
Lesson 34, Section 2
To find the equation of a line
Straight lines will be parallel if they have the same slope. There is no limit, then, to the number of lines with slope 2.
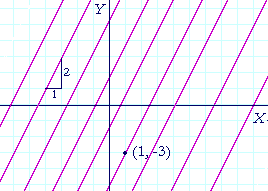
But there will be only one line with slope 2 that passes through a given point, such as (1, −3). In other words, a line will be determined by its slope and the coördinates of one point on it. How can we find the equation of that line?
Problem 1. To write the equation of a line given the slope and the coördinates of one point on it.
For example: Write the equation of the line with slope 2 that passes through the point (1, −3).
Solution 1. The direct method. The equation will have the form
y = ax + b,
where a is the slope of the line.
We are given that a = 2. Therefore, the equation will look like this:
y = 2x + b.
We must now determine b.
To do that, we must use the information that (1, −3) are the coördinates of a point on the line. Those coördinates then solve the equation.
−3 = 2· 1 + b
This implies
b = −5.
The equation of the line is
y = 2x − 5.
Solution 2. The point-slope formula. Let (x, y) be any point on the line. And let (x1, y1) be a specific point on the line.
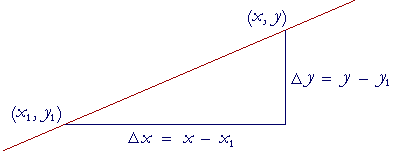
Then if m is the slope of that line, ![]() is equal to that slope
is equal to that slope
![]()
This is called the point-slope formula for the equation of a straight line. We can use the formula when we know the slope m of the line and one point (x1, y1) on it. However, many find the direct method to be simpler.
So, returning to our example, we are given that m = 2 and that
| (x1, y1) | = | (1, −3). |
| Therefore, according to the point-slope formula: | ||
| y − (−3) x − 1 |
= | 2. |
| We must solve this for y: | ||
| y + 3 | = | 2(x − 1) |
| = | 2x − 2. | |
| This implies | ||
| y | = | 2x − 5. |
This is the equation of the line.
Problem 2. To find the equation of a line given the coördinates of two points on it.
For example: Write the equation of the line that passes through the points (−3, 11) and (−5, 15).
Solution 1. The direct method. The only difference between this problem and the previous one is that, here, we must calculate the slope. We did that for those two points in Problem 3b. We found the slope to be −2 The equation, then, will look like this:
y = −2x + b
Again, we must find b by letting one of the given points solve the equation. Let (−3, 11) solve it:
11 = −2· −3 + b
This implies
b = 5.
The equation is:
y = −2x + 5.
Solution 2. Simultaneous equations.
The two points are (−3, 11) and (−5, 15). Let each of them solve the equation, y = ax + b.
1) 11 = −3a + b
2) 15 = −5a + b
According to the methods of Lesson 35, let us eliminate b. We will multiply equation 2) by −1:
2') −15 = 5a − b
On adding, we find
−4 = 2a.
a = −2.
Upon replacing that in Equation 1):
11 = −3(−2) + b.
This implies
b = 11 − 6 = 5.
The equation is
y = −2x +5.
Solution 3. The two-point formula.
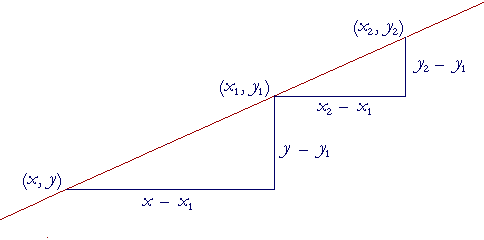
Let (x1, y1) and (x2, y2) be two given points, and let (x, y) be any point on the line. Then the slope joining one of the given points and any point, is equal to the slope joining the two given points, because a line has one and only one slope.
![]()
This is called the two-point formula for the equation of a straight line. We can use it to determine the equation when we know two points. We may choose (x1, y1) to be either one of them.
Thus, in our example, we are given the two points (1, 5) and (4, 17). Let (x1, y1>) be (1, 5). Then according to the two-point formula:
| y − 5 x − 1 |
= | 17 − 5 4 − 1 |
|||
| That is, | |||||
| y − 5 x − 1 |
= | 12 3 |
= | 4 | |
| y − 5 | = | 4(x − 1) | |||
| = | 4x − 4 | ||||
| This implies | |||||
| y | = | 4x + 1. | |||
This is the equation of the line.
Problem 12.
| a) | Write the slope-intercept form of the equation of the line with slope 3, and which passes through the point (1, −4). Use the direct method. |
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
The equation will have the form
y = ax + b,
where a is the slope of the line.
We are given that a = 3. Therefore, the equation is
y = 3x + b.
Now we must determine b.
We are given that (1, −4) is a point on the line. Those coördinates, then, solve the equation:
−4 = 3· 1 + b
This implies
b = −7.
The equation of the line is
y = 3x − 7.
| b) | Write the slope-intercept form of the equation of the line with slope −1, and which passes through the point (−8, −2). Use the point-slope formula. |
We are given that m = −1 and that
| (x1, y1) | = | (−8, −2). |
| Therefore, according to the point-slope formula: | ||
| y − (−2) x − (−8) |
= | −1 |
| We must solve this for y: | ||
| y + 2 | = | −1(x + 8) |
| = | −x − 8 | |
| This implies: | ||
| y | = | −x − 10. |
This is the equation of the line.
Problem 13. Write the equation of the line that passes through (1, −6) and (−1, 2). Use the two-point formula. Let (x1, y1) = (1, −6).
According to the formula:
| y − (−6) x − 1 |
= | 2 − (−6) −1 − 1 |
|||
| That is, | |||||
| y + 6 x − 1 |
= | 8 −2 |
= | −4 | |
| y + 6 | = | −4(x − 1) | |||
| = | −4x + 4 | ||||
| This implies | |||||
| y | = | −4x − 2. | |||
This is the equation of the line.
Next Lesson: Simultaneous linear equations
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com