39
VARIATION
The constant of proportionality
THE SUBJECT OF VARIATION is more properly the subject of arithmetic, because it rests squarely on the concept of ratio. See Skill in Arithmetic, Lesson 17.
Direct variation
We say that a quantity a varies directly as a quantity b, if, when b changes, a changes in the same ratio.
That means that if b doubles in value, a will also double in value. If b increases by a factor of 3, then a will also increase by a factor of 3. While if the value of b becomes half, so will the value of a.
Let the initial values of a and b be a1, b1, and let their final values be
a2, b2. Then, a varies directly as b means: Proportionally,
a2 : a1 = b2 : b1
| " | The final value of a is to the initial value of a |
| as the final value of b is to the initial value of b." | |
Since problems typically ask for the value of a2, then we can make it the 4th proportional.
b1 : b2 = a1 : a2
Example 1. a varies directly as b, and when b = 2, a = 7. What is the value of a when b = 10?
Solution. The value of b has gone from 2 to 10. That is, it has increased five times. Therefore, the value of a will increase five times. It will go from 7 to 35.
Formally,
b1 : b2 = a1 : a2
2 : 10 = 7 : a2
10 is five times 2. Therefore, a2 will be five times 7.
Example 2. a varies directly as b, and when b = 8, a = 4. What is the value of a when b = 13?
Solution. Proportionally,
b1 : b2 = a1 : a2
That is,
8 : 13 = 4 : a2
Alternately, 4 is half of 8. Therefore, a2 will be half of 13, which is 6.5.
Problem 1. a varies directly as b. When b = 12, a = 27. What is the value of a when b = 4? To see the answer, pass your mouse over the colored area.
The value of b has gone from 12 to 4. Its final value, then, is a third of its initial value. Therefore, the final value of a will be a third of 27, which is 9.
Problem 2. When b = 6, a = 42. What is the value of a when b = 9?
b1 : b2 = a1 : a2.
6 : 9 = 42 : a2.
Alternately, 42 is seven times 6. Therefore, a2 will be seven times 9, which is 63.
Or, 9 is one and a half times 6. (6 + 3 = 9.) Therefore, a2 will be one and a half times 42. 42 + 21 = 63. The constant of proportionality When a varies directly as b, we often say, "a is proportional to b." When that is the case, the relationship between a and b takes this algebraic form: a = kb. k is called the constant of proportionality. The circumference C of a circle, for example, is proportional to the diameter D. The constant of proportionality is called π. C = πD. That constant has been the subject of investigation for over 2500 years. In scientific problems, the constant of proportionality is determined by experiment. In what is called Hooke's Law, the force F that a stretched spring exerts is proportional to the distance x that the spring has stretched. F = kx. In other words, the greater the stretch x, the greater the force F.
Example 3. a) For a given spring, F has the value 35 when the spring has stretched Solution. F = kx. That is, 35 = k· 8 Therefore, b) What is the value of F when the spring has stretched 11 inches?
Solution. For that spring, we have determined that F = 4.375 x. Therefore, when x = 11, In general, if a is proportional to b, and a1, b1 are observed values, then a1 = kb1. That implies: Therefore, When a varies directly as b, the constant of proportionality is the quotient of any observed or given values. Note: The units on the right must equal those of a on the left -- distance, time, force, whatever they might be. Since b1 is the denominator:, the units of b will cancel as if they were numbers. See the following problem.
Problem 3. a) The distance d that an automobile travels varies directly as the time t b) The units on the right must be same as those of d on the left, that is, The units of time then cancel, leaving only distance on both sides. In this example, the constant of proportionality is the constant speed of the car: 57.5 miles per hour. c) How far has the car traveled after 7 hours?
d = 57.5 × 7 = 402.5 miles. As for Problems 1 and 2 above, while we could have solved them by finding the constant of proportionality, anyone who has to would show a lack of understanding of direct variation.
Problem 4. Prove: Varies directly is a transitive relation. That is, if a varies directly as b, and b varies directly as c, then a varies directly as c.
If a = k1b, and b = k2c, then a = k1k2c.
Problem 5. If the side of a square doubles, how will the perimeter change?
The perimeter will also double, because the perimeter P varies as the side s. P = 4s. The constant of proportionality is 4.
Problem 6. If the diameter of a circle changes from 6 cm to 12 cm, how will the circumference change?
The circumference will also double, because the circumference varies as the diameter. C = πD.
Problem 7. If the diameter of a circle changes from 6 cm to 9 cm, how will the circumference change?
In going from 6 cm to 9 cm, the diameter has increased one and a half times; that is the ratio of 9 to 6. Therefore, the circumference will also increase one and a half times.
Problem 8. The circumference C of a circle varies directly as the perimeter of the circumscribed square. What number is the constant of proportionality?
Therefore the perimeter of the square is equal to 4D. Varies as the square A quantity a varies as the square of a quantity b means: If b changes by a certain factor Algebraically: If b2 = cb1, then a2 = c2a1. Thus if b changes by a factor of 4, then a will change by a factor of 42 = 16. If b changes to one third of its value, then a will change to one ninth of its value.
Problem 9. a varies as the square of b. When b = 7, a = 4. What is the value of a when b = 35?
In going from 7 to 35, b has changed by a factor of 5. a therefore will change by a factor of 52 = 25. a = 25· 4 = 100.
Problem 10. a varies as the square of b. When b = 20, a = 32. What is the value of a when b = 15?
In going from 20 to 15, b has become three fourths of its value. 15 is three fourths of 20. a therefore will become nine sixteenths of its value.
Theorem. If a varies directly as b, then a2 will vary as b2. This is easily proved if we write the ratios in fractional form. a varies directly as b means: Therefore, on squaring both sides: This implies This means that a2 varies as b2; which is what we wanted to prove.
Problem 11. The area A of a circle varies directly as the area of the circumscribed square. That is, as the area of the square changes, the area of the circle changes proportionally. a) Show that this implies that the area A of the circle varies as the
The side of the circumscribed square is equal to the diameter D of the circle. Therefore the area of the circumscribed square is equal to D2. Hence the area A of the circle varies as D2.
But D varies directly as r : D = 2r; therefore according to the
theorem, D2 varies as r2. Therefore, since A varies as D2, and D2 varies as r2, then transitively, A varies as r2. The area of the circle varies as the square of the radius. b) If the radius of a circle changes from 6 cm to 12 cm, how will the
In going from 6 cm to 12 cm, the radius has doubled, that is, it has changed by a factor of 2. The area therefore will change by a factor of 22 = 4. It will be four times larger. c) What is the constant of proportionality that relates the area A to r2?
π. A = πr2.
Example 4. The surface area of a sphere. The surface area of a sphere is proportional to the surface area of the circumscribed cube. Now, each face of the cube is a square whose side is equal to the diameter D of the sphere. And a cube has 6 faces. Therefore, the surface area of the cube is equal to 6D2. In other words, the surface area A of a sphere is proportional to the square of its diameter. Do you know what the constant of proportionality is?
π. A = πD2
Problem 12. Show that the surface area of a sphere varies as the square of its radius. Write the equation that relates the surface area A to the radius r.
Since A = πD2, and D = 2r, then A = π(2r)2 = 4πr2. Section 2: Varies inversely. Varies as the inverse square. Please make a donation to keep TheMathPage online. Copyright © 2021 Lawrence Spector Questions or comments? E-mail: teacher@themathpage.com
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
a) 8 inches. What is the constant of proportionality for that spring?
k
=
35
8 = 4
3
8 = 4.375
F
=
4.375 × 11
=
43.75 + 4.375 (Skill in Arithmetic, Lesson 9)
=
48.125
![]()
![]()
a) that it travels. After 2 hours, the car has traveled 115 miles. Write
a) the equation that relates d and t.
d
=
115
2t
=
57.5t
a) distance. What are the units, then, of 57.5?
distance
time

π
4. For, the side of the square is equal to the diameter D.
And
C
4D =
1
4·
C
D =
1
4· π
=
π
4.
(which may be greater than or less than 1),
then a will change by the square of that factor.![]()
9
16× 32 = 18
![]()
![]()
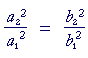

a) square of the radius r.
b) area change?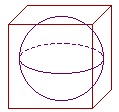
![]()
Even $1 will help.
