Lesson 11 Section 2
Decomposing the dividend
Mental calculation
How much is 42 ÷ 3? That is -- how many 3's are there in 42? Say that you do not know. But you know how many 3's there are in 30 -- ten. And you know how many 3's there are in 12 -- four. Therefore since 42 is composed of 30 + 12 -- you could know that 42 is made up of fourteen 3's.
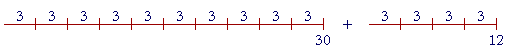
Let us represent that using the division bar:
| 42 3 |
= | 30 + 12 3 |
= | 30 3 |
+ | 12 3 |
= 10 + 4 = 14. |
We have decomposed 42 -- broken it up -- into two numbers that we know are divisible by 3: 30 + 12. They are multiples of 3 that we know.
This can become a simple mental calculation. As always in mental calculation, we go from what we know to what we do not know.
Decomposing the dividend is based on the following, which is one of the most important properties of division. Not only does it enable mental calculation, it is the basis for the written method as well.
If a number is a divisor of two numbers, then it is also
a divisor of their sum and their difference.
| 5. | How do we divide by decomposing the dividend? |
| Break up the dividend into obvious multiples of the divisor. Then divide each multiple, and add or subtract those partial quotients. | |
Example 1. Divide $92 equally among 4 people.
Answer. We have to divide 92 by 4. (Section 1.) We will break 92 up into two numbers that are obviously divisible by 4.
Now, what multiple of 4 is close to 92?
80, for example.
To make 92 we need to add 12. Therefore, we will decompose 92 into 80 + 12:
| 92 4 |
= | 80 4 |
+ | 12 4 |
= | 20 + 3 = 23. |
92 is made up of twenty-three 4's -- which is equal to 4 twenty-three's. Each person will get $23.
Alternatively, we could have broken up 92 as 100 − 8. If we divide each of those by 4, we get 25 − 2 = 23.
Example 2. 265 is made up of how many 5's?
Answer. Again, we go from what we know to what we do not know. Now, which number divisible by 5 is closest to the first two digits of 265?
25. And since 25 is divisible by 5, so is 250. Therefore, decompose 265 as
250 + 15.
Therefore,
| 265 5 |
= | 250 5 |
+ | 15 5 |
= | 50 | + | 3 | = | 53. |
265 is made up of Fifty-three 5's: Fifty 5's + Three 5's.
With a little practice, this will be a mental calculation.
Example 3. 6 CD's that cost the same, together cost $114. How much did each one cost?
Solution.. We have to divide $114 into 6 equal parts.
| 114 6 |
= | 120 − 6 6 |
= | 20 − 1 = 19. |
Each one cost $19.
In this case, it was convenient to decompose 114 as the difference, 120 − 6.
Example 4. A business spent $2,580 on items that cost $6 each. How many such items did they buy?
Answer. What number times $6 will equal $2,580? We must divide 2580 by 6.
Now, since 24 is divisible by 6, then so is 2400.
| 2580 6 |
= | 2400 + 180 6 |
= | 400 + 30 = 430. |
They bought 430 items.
We can check this -- and any division -- by multiplying.
430 × 6 = 400 × 6 + 30 × 6 = 2400 + 180 = 2580.
(Lesson 9)
Example 5. Into how many equal parts of 18 each could you divide 270?
Solution. Which multiple of 18 is 270? According to Problem 5c of Lesson 9, here are the first five multiples of 18:
18, 36, 54, 72, 90.
270, then, which is equal to 180 + 90, is equal to ten 18's plus five 18's. You could divide 270 into fifteen equal parts of 18.
If you happened to know that eighteen 5's are 90, then you would also know that five 18's are 90!
Example 6. Inexact division.
| 22 5 |
= | 20 + 2 5 |
= 4 + | 2 5 |
= 4 | 2 5 |
("Four and two-fifths"). |
| 4 | 2 5 |
is called a mixed number. This is another way of expressing |
inexact division when we are measuring rather than counting. For we need fractions only for measuring.
| In practice, to do | 22 5 |
= 4 | 2 5 |
, say |
"5 goes into 22 four (4) times with 2 left over."
Write the remainder 2 as the numerator of the fraction.
| Example 7. | 99 8 |
= | 80 + 16 + 3 8 |
= 10 + 2 + | 3 8 |
= 12 | 3 8 |
99 has been decomposed into multiples of 8, plus a remainder of 3.
In the next Lesson, we will see that it is on this principle of decomposing the dividend that the historical written method was based.
At this point, please "turn" the page and do some Problems.
or
Continue on to the next Section: Three properties of division.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
