skill

S k i l l
i n
A R I T H M E T I C

Lesson 27 Section 2

Parts of Fractions

Example 1 . A recipe calls for 6 $fraction$ cups of flour, and you are going to make a third of the recipe. How much flour will you use?

Answer. A third of 6 cups is 2 cups. But how much is a third of $fraction$ ?

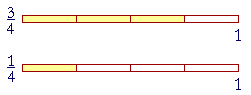
$parts of fractions$

A third of $fraction$ is $fraction$ . Simply take a third of the numerator.

A third of 6 $fraction$ cups is 2 $fraction$ cups.

But say that the recipe calls for 6 $fraction$ cups of flour. Since the numerator 1 does not have a third part, how will you take a third of $fraction$ ?

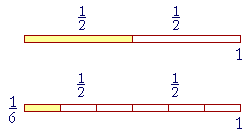
$parts of fractions$

If we divide each $fraction$ into thirds, then the whole 1 will be in three times as many parts. A third of $fraction$ is $fraction$ .

To take a third of a fraction, simply multiply the denominator by 3.

A third of 6 $fraction$ cups is 2 $fraction$ cups.

There are two ways, then, to take a part of a fraction.


4.	How can we take a part of a fraction?

$parts of fractions$

	Take that part of the numerator -- if the numerator has that part.
$parts of fractions$

	If the numerator does not have that part,

$parts of fractions$

	multiply the denominator by the cardinal number that corresponds to the part. That is, to take half, multiply the denominator by 2; to take a third, multiply by 3; and so on.

$parts of fractions$

Example 2.

Half of	6 7	is	3 7	.	Take half of the numerator.

A third of	6 7	is	2 7	.	Take a third of the numerator.

A third of	4 7	is	4 21	.	4 does not have a third part. Therefore multiply the denominator by 3.

Example 3. How much is a fifth of

1
2

Answer.

1
10

. Multiply 2 by 5.

Example 4. How much is half of

1
10

Answer.

1
20

. Multiply 10 by 2.

Example 5.

1
8

is which part of

1
2

Answer. Since 8 is 4 × 2,

1
8

is the fourth part, or one quarter, of

1
2

Example 6.

1
16

is which part of

1
8

? What ratio has

1
32

1
8

Answer.

1
16

is half of

1
8

. 16 = 2 × 8.

1
32

is a fourth of

1
8

. 32 = 4 × 8.

Example 7. Percent. Since

1
8

is half of

1
4

(8 = 2 × 4),

and since

1
4

is equal to 25%, then what percent is

1
8

Answer. Half of 25%, which is 12½%. (Lesson 16, Example 4.)

Now, each eighth will be another 12½%.

2
8

1
4

= 12½% + 12½% = 25%.

3
8

25% + 12½% = 37½%.

4
8

1
2

= 50%.

5
8

50% + 12½% = 62½%.

6
8

3
4

= 75%.

7
8

75% + 12½% = 87½%.

See Problem 15.

Example 8.

2
5

is larger than

2
25

. (Lesson 23, Question 1.) How many

times larger?

Answer. Five times larger. Because 25 is 5 × 5.

Example 9. The following problem appeared in a recent textbook:

1
5

1
2

of what number?

The writer no doubt intend it to be translated as

1
2

times what number is

1
5

-- thus making it a division problem:

1
5

1
2

However, if we make verbal sense of the problem --

1-fifth is half of what number?

-- then the answer is obvious. Just as 1 apple is half of 2 apples, so

1-fifth is half of 2-fifths.

Example 10.

3
7

is half of what number?

Answer.

3
7

is half of

6
7

Example 11.

3
7

is a third of what number?

Answer.

3
7

is a third of

9
7

, which is 1

2
7

Example 12. To make an orange dye, 3 parts of red dye are mixed with 2 parts of yellow dye. To make a green dye, 2 parts of blue dye are mixed with 1 part of yellow dye. If equal amounts of orange and green are mixed, what fraction of the new mixture is yellow dye?

Solution. For convenience, let

O = Orange dye, R = Red dye, Y = Yellow dye,

G = Green dye, B = Blue dye.

Now, the orange dye consists of a total of five parts: 3 parts red and 2 parts yellow. That is,

3
5

R +

2
5

The green dye consists of three parts: 2 parts blue and 1 part yellow.

2
3

B +

1
3

To add equal amounts of O and G, we may simply add half of each. Therefore, half of O is

3
10

R +

1
5

And half of G is

1
3

B +

1
6

Upon adding those equal parts of O and G, the new mixture will consist of

3
10

R +

1
5

Y +

1
3

B +

1
6

The LCM of those fractions is 30. (Lesson 23.) The fractions of Y --

1 5	Y +	1 6	Y

-- become
6 30	Y +	5 30	Y =	11 30	Y.

(Lesson 22, Question 3.)

11
30

is the fraction of yellow dye in the new mixture.

Consider "Half of

5
8

" -- which we know is

5
16

-- and let us write it in

symbols as

1
2

5
8

We now see why we multiply the numerators and multiply the denominators:

1
2

5
8

5
16

It follows, as it must, from what the symbols mean.

Similarly, Half of

6
8

becomes

1
2

6
8

3
8

"2 goes into 6 three (3) times."

Example 13. How much is a third of

5
7

? How much is two thirds?

Answer.

A third of

5
7

5
21.

(Multiply the denominator by 3).

Two thirds of

5
7

is twice as much as one third: 2 ×

5
21

10
21

In symbols,

2
3

5
7

10
21

"Two thirds of

5
7

10
21

And so we have arrived where we began (Lesson 26, Question 3), at the formal rule for multiplying fractions:

Multiply the numerators and multiply the denominators.

Please "turn" the page and do some Problems.

Continue on to Section 3.

Section 1.

1st Lesson on Multiplying Fractions

Introduction | Home | Table of Contents

Questions or comments?

E-mail: teacher@themathpage.com