Lesson 2 Section 2
Place value numeration
THE ORGANIZING PRINCIPLE in our system of naming and writing numbers are the powers of 10. When we write '2,364' for example, we mean the sum of
2 Thousands + 3 Hundreds + 6 Tens + 4 Ones.
This illustrates that, starting with the Ones on the right, we have chosen the powers of 10 to be the units. There are 2 of that unit (Thousands), plus 3 of that unit (Hundreds), plus 6 of that one (Tens), plus 4 of those (Ones). When we write the number, however, we omit the names of the units and the + signs, and just write
2,364.
After the Ones on the right, each place has for its value the next power of 10. We call such a system place value, or positional, numeration.
| 5. | To which place does each digit belong? Equivalently, what is the unit at each position? |
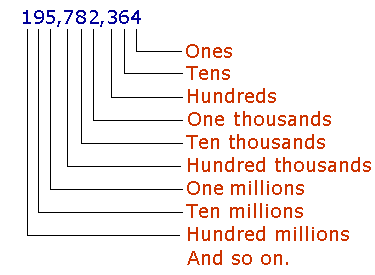 |
|
| Starting with the Ones on the right, each place belongs to the next power of 10. | |
Example 1. In this number,
139,072,658
the 0 is in which place?
Answer. Hundred thousands.
For in each class of three digits, there are Ones, Tens, and Hundreds.
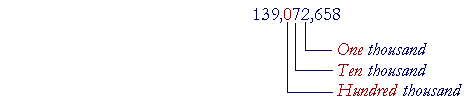
0 is in the class of thousands and in the Hundreds place. The power of 10 at that position is Hundred thousands.
Example 2. In this number,
386,214,035
how many Ten millions are there? That is, which digit is in the ten millions place?
Answer. 8. For on counting from the right, the millions are the third group of three digits, 386. The Tens place is the middle one (Ones, Tens, Hundreds). There are 8 Ten millions.
Place value versus absolute value of a digit
In addition to speaking of a digit being "in" a place, we also speak of the place value of the digit itself. In this number,
6,666
each digit has the same absolute or invariable value 6, but a different place value. 6 on the extreme left has the place value 6000; the next 6 has the value 600; the next, 60; and the last, 6.
Expanded form
The numeral for every whole number stands for a sum.
364 = 3 Hundreds + 6 Tens + 4 Ones.
(Even a single digit stands for a sum: 5 = 1 + 1 + 1 + 1 + 1.)
What is written above is called the expanded form of 364.
| 6. | What does it mean to write a number in expanded form? |
| It means to write the sum that the number indicates, and therefore to name the unit at each digit's place. | |
Example 3. Write 6,325 in expanded form.
Answer. Write
6,325 = 6 Thousands + 3 Hundreds + 2 Tens + 5 Ones.
In practice, however, it is often more useful to expand the number in this way:
6,325 = 6,000 + 300 + 20 + 5.
Example 4. Write the expanded form of 10,000.
Answer. 10,000 = 1 Ten-thousand + 0 Thousands + 0 Hundreds + 0 Tens + 0 Ones.
Example 5. No matter what the unit:
| 42 | = | 40 + 2. | |
| 42 eggs | = | 40 eggs + 2 eggs. | |
| 42 tens | = | 40 tens + 2 tens. | |
| 42 hundreds | = | 40 hundreds + 2 hundreds. | |
And so on. For there is no "42" apart from 42 units, even though we do not say the word units.
Units of adjacent place value
The following question is to prepare for the standard written methods of addition and subtraction. The answer follows from the fact that each digit
6,325
has a place value ten times the digit to its right.
For, each power of 10 is ten times the one to its right:
1000 100 10 1
1000 is made up of ten 100's.
100 is made up of ten 10's.
10 is made up of ten 1's.
And so on.
| 7. | What is the relationship between units of adjacent place value? |
| 1000 100 10 1 | |
| Ten units of lower place value can be composed -- grouped together -- to make one unit of the next higher value. | |
| Equivalently: One unit of higher place value can be decomposed -- broken up -- into ten units of the next lower value. | |

Ten 1's can be composed into one 10.
Ten 10's can be composed into one 100.
Ten 100's can be composed into one 1000.
And so on.
Conversely:
1000 100 10 1
One 1000 can be decomposed into ten 100's.
One 100 can be decomposed into ten 10's.
One 10 can be decomposed into ten 1's.

1000 100 10 1

We will see this when we come to regrouping in addition and subtraction.
Rounding off
| 8. | How do we round off, or approximate, a whole number to a given place? |
1267 1300 1300 | |
| Look at the digit to the right of the given place: hundreds for example (2). If the digit to the right is a 5 or greater, add 1 to the given place. If it is less than 5, leave the given place unchanged. In either case, replace all the digits to the right of the given place with 0's. | |
Example 6. Round off 6,528 to the nearest ten.
Answer. 6,528 6,530
6,530
(The wavy equal sign means "is approximately equal to.")
means "is approximately equal to.")
2 is in the tens place. To round off to the nearest ten, look at the digit to the right: 8 (greater than 5). Therefore, add 1 to the tens place. Replace 8 with 0.
Example 7. Round off 6,528 to the nearest hundred.
Answer. 6,528 6,500
6,500
5 is in the hundreds place. To round off to the nearest hundred, look at the digit to the right: 2 (less than 5). Therefore, leave the hundreds place unchanged. Replace 28 with 00.
Example 8. Round off 6,528 to the nearest thousand.
Answer. 6,528 7,000
7,000
6 is in the thousands place. To round off to the nearest thousand, look at the digit to the right: 5. Therefore, add 1 to the thousands place. Replace 528 with 000.
Example 9. Round off 79,521 to the nearest thousand.
Answer. 79,521 80,000
80,000
9 is in the thousands place. To round off to the nearest thousand, look at the digit to the right: 5. Therefore, add 1 to 79 -- it becomes 80. Replace 521 with 000.
To round off decimals, see Lesson 11.
At this point, please "turn" the page and do some Problems.
or
Continue on to the next Section.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
