Lesson 17
RATIO AND PROPORTION
Ratio is the spoken language of arithmetic. It is how we relate quantities of the same kind.
6 people, for example, are half of 12 people. "Half" is the name of the ratio -- the relationship -- of 6 to 12. Most important, we will see that percents are ratios. In the language of percent, we say that 6 people are 50% of 12 people. Why? Because 50% has that same ratio to 100%. "Half."
This Lesson depends on Lesson 15: Parts of Natural Numbers
In this Lesson, we will answer the following:
- What do we mean by the ratio of two natural numbers?
- How do percents name ratios?
- What is a proportion?
- How can we express the ratio of any smaller number to a larger number?
- When is a ratio expressed with the lowest terms?
- How can we know when a ratio is expressed with the lowest terms?
- What is the theorem of the common divisor?
| 1. | What do we mean by the ratio of two natural numbers? |
| It is their relationship with respect to relative size, which we can always name. Specifically, we can say that one number is a multiple of the other (so many times it), a part of it, or parts of it. | |
(After Euclid, Book VII. Def. 20.)
Example 1. Multiple. What ratio has 15 to 5?
Answer. 15 is three times 5.
That is the ratio -- the relationship -- of 15 to 5. If Jill has $15, and Jack has $5, then Jill has three times more than Jack.
To answer "3 to 1" is not sufficient, because we want to name the ratio of 15 to 5 explicitly. It is true that 15 is to 5 as 3 is to 1 -- but what ratio has 3 to 1?
3 is three times 1.
(The 19th century program to rid mathematics of language and replace it with formal, algebraic relations, successfully put to sleep the subject of ratio and proportion.)
Notice that we answer with a complete sentence beginning with the first number 15, and ending with the last number 5. For a ratio is a relationship.
The two numbers in a ratio are called the terms; the first and the second.
When the first term is larger, we say it is so many times the smaller. 15 is three times 5.
What ratio has 28 to 7?
28 is four times 7.
Example 2. Part. What ratio has 5 to 15?
Answer. 5 is the third part of 15.
That is called the inverse ratio of 15 to 5. The terms are exchanged.
Notice again that we answer with a complete sentence beginning with the first term and ending with the second. "5 is 15."
Example 3. Parts. What ratio has 10 to 15?
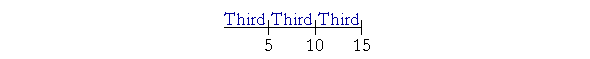
Answer. 10 is two thirds of 15.
"Three times." "The third part." "Two thirds." Those are names of ratios; of relations between two numbers. One number is a multiple of the other (so many times it), a part of it, or parts of it.
As we pointed out in the Lesson on parts, the names of ratios are prior to the names of the proper fractions.
Example 4. What ratio has 12 to 6?
Answer. 12 is two times 6. Or we could say, "12 is twice as much as 6," or "12 is double 6."
Those are the various ways of expressing the ratio, the relationship, of 12 to 6.
Inversely, 6 is half of 12.
When trying to express a ratio, if the student will say a sentence, and then consider the truth of that sentence, the fact will speak for itself.
Example 5. What ratio has 80 to 8? Inversely, what ratio has 8 to 80?
Answer. 80 is ten times 8. Therefore, inversely, 8 is that part of 80 with the ordinal form of ten: 8 is the tenth part of 80.
(For the relationship between 8 and 8-with-a-0 after it, i. e. 80, see Lesson 2 and the problems that follow.)
Example 6. What ratio has 800 to 8? Inversely, what ratio has 8 to 800?
Answer. 800 is one hundred times 8. Inversely, 8 is the hundredth part of 800.
Percents are ratios
A percent names a relationship between two number. 6 is 50% of 12. Therefore a percent is another way of naming a ratio.
What ratio has 3 to 12? 3 is one quarter of 12. In the language of percent, 3 is 25% of 12. Why does 25% mean one quarter? Because 25% is one quarter of 100%. (Lesson 15.)
| 2. | How do percents name ratios? |
| Whatever ratio the percent has to 100%, that is the ratio being named. | |
Example 7. What does 200% mean?
Answer. Since 200% is two times 100%, then 200% means two times. 200% of 8 -- two times 8 -- is 16.
Example 8. How much is 300% of 8?
Answer. 24. 300% of 8 means three times 8 because 300% is three times 100%.
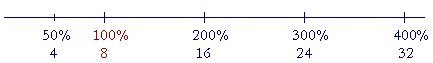
100% is the whole, in this case, 8. 50% means half, because 50% is half of 100%. 50% of 8 is 4.
200% means two times; 300% means three times; 400% means four times; and so on.
Whatever ratio the percent has to 100%, that is the ratio being named.
We see that any number less than 8 will be less than 100% of 8. While any number more than 8 will be more than 100%.
We have, as it were, two languages: The language of ratio -- "Half," "Three quarters," "Twice as much" -- and the language of percent: 50%, 75%, 200%. The student must become fluent in both languages, and in translating from one to the other.
Example 9. Compare the following:
a) 10 has what ratio to 40? b) 10 is what percent of 40?
c) 7 has what ratio to 21? d) 7 is what percent of 21?
Answers. a) 10 is the fourth part of 40, or a quarter of 40, or a fourth of 40.
b) 10 is 25% of 40.
25% means a quarter, because 25% is a quarter of 100%.
| c) 7 is a third of 21. d) 7 is 33 | 1 3 |
% of 21. | Lesson 16, Question 6. |
Example 10. How much is 250% of 8?
Answer. 250% means two and a half times. It is 200% + 50%. 250% is a mixed number of times -- expressed as a percent.
250% of 8, therefore, is 16 + 4 = 20.
| Example 11. How much is 433 | 1 3 |
% of $60? |
| Answer. 433 | 1 3 |
% = 400% + 33 | 1 3 |
%: Four and a third times. |
| 433 | 1 3 |
% of $60 = $240 + $20 = $260. |
Example 12. Calculate mentally: 125% of $7.80.
Answer. 125% means one and a quarter times: 100% + 25%.
100% of $7.80 is $7.80.
To take a quarter of $7.80, we can decompose it into two numbers that clearly have a quarter.
$7.80 = $8.00 minus 20 cents.
A quarter of $8.00 is $2.00.
A quarter of 20 cents is 5 cents.
Therefore,
| 125% of $7.80 | = | $7.80 + $2.00 − 5 cents |
| = | $9.80 − 5 cents | |
| = | $9.75. | |
Percent continues in Lesson 18.
"as many"
Example 13. "There are a fifth as many green marbles as red ones."
What does that mean?
It means that the number of greens is a fifth of the number of reds. So if there were 15 reds, there would be 3 greens.
"a fifth" is the name of a ratio. It immediately precedes "as many."
In the language of percent, "There are 20% as many green marbles as red ones."
With any percent problem, immediately translate into the language of ratio.
"There are 75% as many boys in the class as girls."
Translate: "There are three quarters as many boys as girls."
If there were 20 girls, there would be 15 boys.
Practice with these problems continues in Lesson 28.
At this point, please "turn" the page and do some Problems.
or
Continue on to the next Section: Proportions
1st Lesson on Parts of Natural Numbers
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
