Book I, Proposition 4
Problems
Back to Proposition 4.
1. What are the three magnitudes of plane geometry?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Length, area, and angle.
2. What kind of a magnitude is a triangle? Area.
2. b) What would it mean to say that two triangles are equal?
That they are equal areas.
2. c) Are equal triangles necessarily congruent?
No. Triangles may be equal areas without coinciding.
2. d) Are congruent triangles necessarily equal? Yes.
3. a) State the converse of Axiom 4.
Things that are equal to one another coincide with one another.
3. b) Is the converse true? No.
4. a) State the hypothesis of Proposition 4.
Two triangles have two sides equal to two sides respectively, and the angles contained by those sides are also equal.
4. b) State the conclusion.
The remaining side is equal to the remaining side, the triangles are equal areas, and those angles are equal that are opposite the equal sides.
5. Figure ABC is a circle with center D; ABC is a triangle with base
5. BDC; and AD is perpendicular to BC. Prove that AB is equal to AC.

Triangles ADB, ADC are congruent. For, BD is equal to DC, because they are radii of the circle. (Definition 15.)
Angle ADB is equal to angle ADC, because all right angles are equal. (Definition 3, and Postulate 4.)
And AD is a common side of triangles ADB, ADC. Therefore -- S.A.S. -- the remaining side AB is equal to the remaining side AC.
6. In this figure, EF is equal to GH, and angle EFH is equal to angle
6. GHF. Prove that triangles EFH, GHF are equal areas, and that angle
6. EFH is equal to angle GHF.
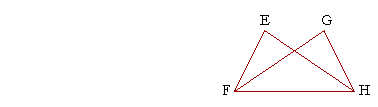
By hypothesis, EF is equal to GH, and angle EFH is equal to angle GHF.
And FH is a common side of triangles EFH, GHF.
Therefore -- S.A.S. -- those triangles are congruent and therefore equal areas.
Further, in triangle EFH, the remaining side EH is equal to GF, the remaining side in triangle GHF;
and those angles are equal that are opposite the equal sides;
therefore angle EFH (opposite side EH) is equal to angle GHF (opposite the equal side GF).
7. ABC is a triangle, AB is equal to AC, and AE is equal to AD. Prove
6. that triangles AEB, ADC are equal, and that angle AEB is equal to
5. angle ADC.
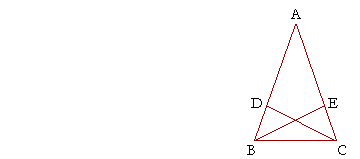
In the overlapping triangles AEB, ADC, the sides BA, AE are equal to the sides CA, AD respectively, by hypothesis.
And angle DAE is common to both triangles.
Therefore -- S.A.S. -- triangles AEB, ADC are congruent and therefore equal.
Further, those angles are equal that are opposite the equal sides: angle AEB (opposite side AB) is equal to angle ADC (opposite the equal side AC).
Table of Contents | Introduction | Home
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com