Book I. Proposition 15
Problems
Back to Proposition 15.
1. PQ, RS are straight lines that intersect at T. Name two pairs of
1. vertical angles.
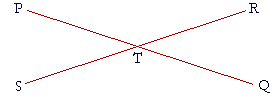
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
Angles PTR, STQ, and angles RTQ, PTS.
2. a) State the hypothesis of Proposition 15.
Two straight lines intersect one another.
2. b) State the conclusion.
The vertical angles are equal.
2. c) Practice Proposition 15.
3. Straight lines AC, DB intersect at E, at which both lines are bisected.
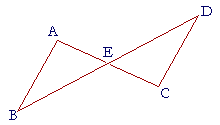
Prove that AB is equal to DC, and that angle A is equal to angle C.
By hypothesis, AE is equal to EC, and DE is equal to EB;
and angle DEC is equal to angle AEB, because they are vertical angles;
therefore the remaining side BA of triangle BAE is equal to the remaining side CD of triangle CDE (S.A.S.).
And those angles are equal that are opposite the equal sides. Therefore angle A, opposite side BE, is equal to angle C, opposite the equal side ED.
Table of Contents | Introduction | Home
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com