Book I. Propositions 18 and 19
Problems
Back to Propositions 18 and 19.
1. a) In triangle ABC, side BC is the longest side. Name the largest
1. b) angle.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
Angle BAC.
1. b) In triangle ABD, angle BDA is the largest angle. Name the
1. b) longest side.
Side AB.
2. a) State the hypothesis of Proposition 18.
In a triangle one side is greater than another side.
2. b) State the conclusion.
The greater angle is opposite that greater side.
2. c) Practice Proposition 18.
3. a) State the hypothesis of Proposition 19.
In a triangle one angle is greater than another angle.
2. b) State the conclusion.
The greater side is opposite that greater angle.
2. c) Practice Proposition 19.
4. In triangle ABC, side BC has been extended to D.
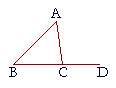
4. a) Why is angle ABC less than angle ACD?
Proposition 16: The exterior angle of a triangle is greater than either of the opposite interior angles.
4. b) If we join angle ACB to both angle ABC and angle ACD, what
4. b) may we conclude?
The two angles ABC, ACB are together less than the two angles ACD, ACB, that is, they are less than two right angles. For angles ACD, ACB are together equal to two right angles. (I. 13)
4. b) This is Proposition 17: Any two angles of a triangle are together less
4. b) than two right angles.
4. b) There is the tacit assumption: If equals are added to unequals,
4. b) the sums will be unequal in the same sense; if less than, then less than, and if
4. b) greater, greater.
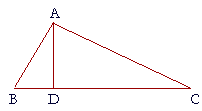
5. In triangle ABC, the angle A is bisected by the straight line AD that
5. meets BC at D.
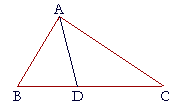
Prove that AB is greater than BD, and that AC is greater than CD.
(In approaching this problem, the student should ask, How can we
5. possibly prove that one side is greater than another? And how can
5. we use the information given?)
Angle BDA is exterior to triangle ACD; therefore it is greater than the opposite interior angle DAC. (I. 16)
But angle DAB is equal to angle DAC; (Hypothesis)
therefore angle BDA is also greater than angle DAB.
And a greater angle is opposite a greater side;
therefore side AB is greater than side BD.
In the same way, we can prove that angle CDA is greater than angle DAC;
therefore side AC is greater than side CD.
Table of Contents | Introduction | Home
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com