Book I. Proposition 26
Problems
Back to Proposition 26.
1. Name three sets of sufficient conditions for triangles to be congruent.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
Side-angle-side.
Side-side-side.
Angle-side-angle.
Or equivalently,
Side-angle-angle.
2. a) State the hypothesis of Proposition 26.
Two triangles have two angles equal to two angles respectively, and one side equal to one side, which may be either the sides between the equal angles or the sides opposite one of them.
2. b) State the conclusion.
The remaining sides will equal the remaining sides (namely those that are oppostie the equal angles), and the remaining angle will equal the remaining angle.
2. c) Prove the second case in which the sides opposite one of the
2. c) angles are equal.
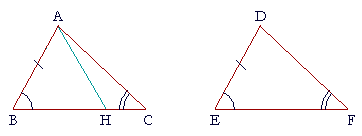
2. c) That is, let angles B and C be equal respectively to angles E and F,
2. c) and let AB equal DE.
2. c) Prove that BC is equal to EF.
If they are not equal, then assume that BC is greater; make BH equal to EF, and draw AH.
Then triangles ABH, DEF are congruent. (S.A.S.)
Therefore angle AHB is equal to angle DFE.
But, by hypothesis, angle ACB is equal to angle DFE.
Therefore, angle AHB is also equal to angle ACB,
which is impossible (I. 16).
Therefore BC is not unequal to EF. It is equal to it.
3. In quadrilateral ABCD, angles CDB, DBA are equal, and angles
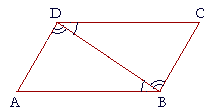
3. ADB, DBC are equal. Prove that AD is equal to BC.
Since angles ADB, DBA are equal respectively to angles DBC, CDB,
and side DB is common to triangles DBA, DBC,
then the remaining sides are equal (A.S.A.),
namely those that are opposite the equal angles;
side AD is equal to side BC.
4. In the rectangle ABCD, angle ABD is equal to angle BDC.
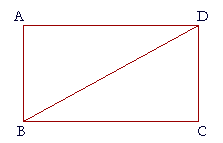
4. Prove that angle ADB is equal to angle DBC.
4. (A rectangle is a quadrilateral in which all the angles are right angles.)
The right angle at A is equal to the right angle at C,
because all right angles are equal.
And angle ABD is equal to angle BDC, by hypothesis.
In triangles ABD, BDC, then, angles DAB, ABD are equal respectively to angles DCB, BDC;
and side DB is common;
therefore the remaining angles are equal (A.A.S.);
angle ADB is equal to angle DBC.
5. In this figure, the angles at B and C are right angles, the straight line
5. BC is bisected at D, and ADE is a straight line. Prove that AB is
5. equal to CE.
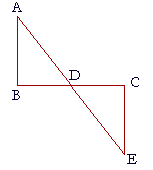
Angle BDA is equal to angle CDE; (I. 15)
angle B is equal to angle C; (Postulate 4)
and BD is equal to DC. (Hypothesis)
Therefore triangles BDA, CDE are congruent, (A.S.A.)
and those sides are equal that are opposite the equal angles:
side AB is equal to side CE.
6. Use Proposition 26 to prove Proposition 6 directly:
6. If two angles of a triangle are equal, then the sides opposite those angles
6. will be equal.
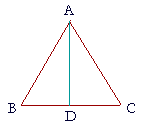
6. In triangle ABC, let angle B equal angle C; then side AB is equal
6. to side AC.
(Hint: Draw the straight line AD that bisects angle A. (I. 9.)
Angle B is equal to angle C, (Hypothesis)
angle BAD is equal to angle CAD, by construction,
and side AD is common to triangles BAD, CAD.
Therefore those triangles are congruent (A.A.S.),
and therefore the remaining sides are equal:
side AB is equal to side AC.
The following problems will depend on proving congruence; either S.A.S., S.S.S., A.S.A. or S.A.A.
7. Prove: The straight line that bisects the vertex of an isosceles triangle also
7. bisects the base and is perpendicular to it.
7. (That is, it is the perpendicular bisector of the base.)
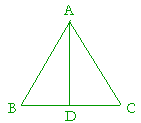
Let triangle ABC be isosceles with side AB equal to side AC;
let the straight line AD bisect angle A;
then BD is equal to DC,
and angles ADB, ADC are right angles.
For, in triangles BAD, CAD two sides and their included angles are respectively equal;
therefore the remaining side is equal to the remaining side:
BD is equal to DC. (S.A.S.)
And those angles are equal that are opposite the equal sides;
angle ADB is equal to angle ADC.
And since they are adjacent angles they are right angles.
This is what we wanted to prove.
8. In quadrilateral ABCD, the straight line AC is the perpendicular
8. bisector of the straight line BD at the point E.
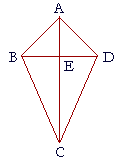
9. a) Prove that triangles ABD and BCD are both isosce1es.
BE is equal to ED; (Hypothesis)
angles AEB, AED are right angles, (Hypothesis)
therefore they are equal;
and AE is common to triangles AEB, AED.
Therefore the remaing side is equal to the remaining side:
AB is equal to AD. (S.A.S.)
Triangle ABD therefore is isosceles. (Definition 8)
Next, in triangles BEC, DEC, the right angles BEC, DEC are equal;
side BE is equal to side ED,
and EC is a common side.
Therefore the remaing side is equal to the remaining side:
BC is equal to DC. (S.A.S.)
Therefore triangle BCD is isosceles.

9. b) Prove that angle ABC is equal to angle ADC.
Since triangles DAB, BCD are isosceles,
the angles at the base, angles ABD, ADB are equal,
and angles CBD, CDB are equal. (I. 5)
Therefore angles ABE, EBC together are equal to angles ADE, EDC together; (Axiom 2)
angle ABC is equal to angle ADC.
19. BDEC is a straight line, AB is equal to AC, and AD is equal to AE.
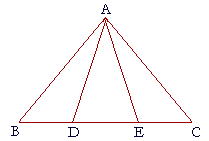
19. Prove that BD is equal to EC.
We will show that triangles ADB, AEC are congruent. First,
since AD is equal to AE, (Hypothesis)
angle ADE is equal to angle AED
because triangle ADE is isosceles.
Therefore angle ADB is equal to angle AEC,
because they are supplements of equal angles.
(I. 13, Problem 6)
Next, side AB is equal to side AC; (Hypothesis)
therefore in the isosceles triangle ABC, angle B is equal to angle C;
and we have shown angle ADB equal to angle AEC;
therefore in triangles ADB, AEC the remaining sides are equal:
BD is equal to EC. (S.A.A.)
10. Angles EBA and CBD are right angles. EB is equal to BA, and DB
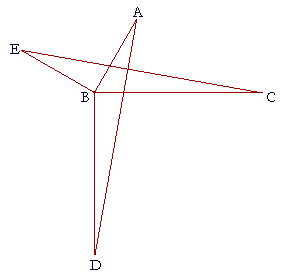
is equal to BC. Prove that triangles EBC, ABD are congruent.
Angle EBA is equal to angle CBD
because they are right angles.
To each of them join angle ABC;
then angle EBC is equal to angle ABD.
Next, side EB in triangle EBC is equal to side AB in triangle ABD,
and side BC is equal to side BD. (Hypothesis)
Therefore two sides and the included angle of triangle EBC are equal respectively to two sides and the included angle of triange ABD.
Therefore those triangles are congruent. (S.A.S.)
Table of Contents | Introduction | Home
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com