Book I. Propositions 31 and 32
Problems
Back to Propositions 31, 32.
11. Solve the problem of Proposition 31:
Through a given point to draw straight line parallel to a given straight line.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
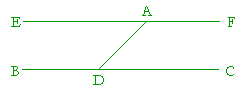
Let A be the given point, and BC the given straight line;
we are required to draw a straight line through the point A parallel to BC.
Choose any point D on BC, and draw AD;
at the point A construct an angle DAE equal to angle ADC; (I. 23)
and extend EA to F.
Then EF will be parallel to BC. For,
the straight line AD, which meets the two straight lines EF, BC makes the alternate angles EAD, ADC equal. Therefore EF is parallel to BC. (I. 27)
12. a) State the hypothesis of Proposition 32.
A figure is a triangle and one side is extended.
2. b) State the conclusion.
The exterior angle is equal to the two opposite interior angles; and the three interior angles of a triangle are equal to two right angles.
2. c) Practice Proposition 32.
13. Prove Proposition 32 by drawing a straight line DE through A
13. parallel to BC.
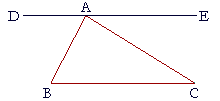
3. This proof is attributed to Pythagoras, who lived some 250 years
3. before Euclid.
Because DE is parallel to BC,
the angle DAB is equal to ABC,
because they are alternate angles;
for the same reason, angle EAC is equal to ACB.
Angles DAB, BAC, CAE are together equal to two right angles. (I. 13)
Therefore the three angles of the triangle, ABC, BCA, CAB, are together equal to two right angles.
14. ABC is a circle with center D; ABD is a triangle; and ADC is a
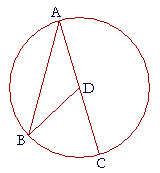
14. straight line. Prove that angle BDC is double angle A.
AD is equal to DB because they are radii of the circle;
therefore angle B is equal to angle A. (I. 5)
The exterior angle BDC is equal to the two opposite interior angles together,
angles A and B; (I. 32);
therefore, angle BDC is double angle A.
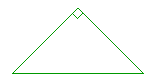
15. Prove: The acute angles of a right triangle are together equal to a
15. right angle.
The three angles of a triangle are equal to two right angles,
and the right angle itself accounts for one of them;
therefore, the remaining two angles together must equal one right angle.
This also implies that each of them must be less than a right angle, an acute angle.
16. In an isosceles right triangle, why is each acute angle half of a right
19. angle?
Since the triangle is isosceles, the base angles are equal.
But together they equal one right angle.
Therefore each one is half of a right angle.
17. Prove that if an acute angle of one right triangle is equal to an acute
17. angle of another, then the remaining acute angles are also equal.
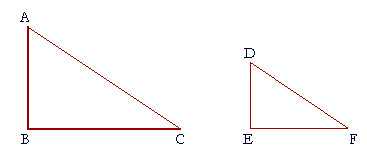
That is, if angles B and E are right angles, and angle C equals
17. angle F, then angle A is equal to angle D.
Angles A and C together equal one right angle,
as do angles D and F;
therefore angles A and C are equal to angles D and F. (Axiom 1)
But angle C is equal to angle F;
therefore on subtracting them from those pairs of equals,
the angles that remain are equal; (Axiom 3)
angle A is equal to angle D.
18. According to the Corollary to I. 32, the four interior angles of any
18. quadrilateral are equal to how many right angles?
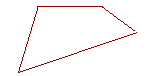
Four.
19. In any five-sided rectilineal figure, the five angles are together equal
19. to how many right angles?
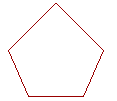
Six.
10. In the degree system of angular measurement, in which a right angle
10. is called 90°, how many degrees is each angle in a regular octagon?
10. (That is an eight-sided figure which is both equilateral and
10. equiangular.)
135°
Table of Contents | Introduction | Home
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com