First Principles
Problems
Back to First Principles.
1. a) If you are told, "Figure ABC is a triangle," what information does
1. a) that give you?

To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
According to the definition of a triangle, you would know that AB, BC, and CA are straight lines.
1. b) Which Postulate guarantees that a triangle could actually exist?
Postulate 1, because it grants that we may draw a straight line between any two points.
2. Complete the following with the name of a straight line.
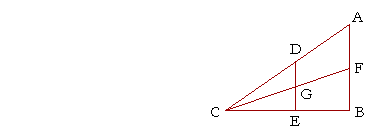
1. a) AB is equal to AF added to FB.
1. b) If GF is added to CG, then the whole is CF.
1. c) If DA is subtracted from to CA, then what remains is CD.
1. d) If EC is subtracted from to BC, then what remains is BE.
1. e) GE added to DG is equal to DE.
3. Adjacent angles have a common vertex and a common side between
3. them.
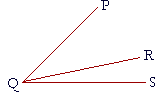
Angles PQR, RQS are adjacent. They have a common vertex Q,
3. and RQ is the common side between them.
3. Note that we name an angle by naming three letters; angle PQR,
3. or angle RQP, it does not matter: except that the middle letter must
3. correspond to the vertex of the angle, which is the point where the
3. two lines PQ, QR meet.
3. In the figure below, name all pairs of adjacent angles.
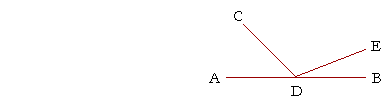
Angles ADC, CDE.
Angles ADC, CDB.
Angles ADE, EDB.
Angles CDE, EDB.
4. AB, DC are straight lines that intersect at E. How many pairs of
3. adjacent angles can you name?
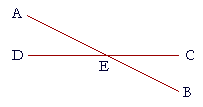
Angles AED, AEC.
Angles AED, DEB.
Angles DEB, BEC.
Angles BEC, CEA.
5. Complete the following by naming an angle.
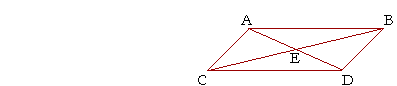
5. a) Angle CAB is equal to angles CAD, DAB together.
5. b) Angle ACD is equal to angles ECD, ACE together.
5. c) Angle EBD together with angle EBA is equal to angle ABD.
4. d) If angle ACB is subtracted from angle ACD, then what remains is
5. d) angle
BCD.
5. e) If angle ADB is subtracted from angle CDB, then what remains is
5. d) angle
ADC.
6. a) In this figure, angles ABD, DBE together are equal to angle ABE.
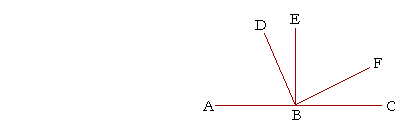
5. b) If angle CBF is subtracted from angle CBD, which angle remains?
Angle FBD.
5. c) If angle DBA is subtracted from angle FBA, which angle remains?
Angle FBD.
7. Angles ABC, CBD are right angles.
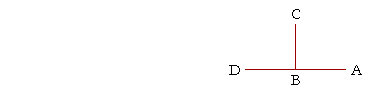
6. How would we know that they are right angles?
There is only one way to answer such a question: Quote the definition of a right angle.
Thus, angles ABC, CBD are "right angles" because the straight line CB is standing on the straight line AD, and the adjacent angles ABC, CBD are equal.
8. Figure ABC is a circle; that is, the points A, B, C lie on the

2. circumference. D is the center, and AD, DC are straight lines.
8. Why is AD equal to DC?
Because, according to the definition of a circle, AD and DC are straight lines drawn from the center to the circumference -- they are radii -- and therefore they are equal.
Table of Contents | Introduction | Home
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com