Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

THE DUPLICATION OF AN ANGLE
Book I. Propositions 22 and 23
IT IS NOT POSSIBLE to construct a triangle out of just any three straight lines, because any two of them taken together must be greater than the third. (Proposition 20.) Here then is the problem of constructing a triangle out of three given straight lines.
PROPOSITION 22. PROBLEM
| To construct a triangle whose sides are equal to three given straight lines: thus any two of them taken together must be greater than the third. | |
| Let A, B, C be the three given straight lines, and let any two of them taken together be greater than the third; namely, | |
| A, B greater than C, | |
| A, C greater than B, | |
| B, C greater than A; | |
| we are required to construct a triangle whose sides are equal to A, B, C. | |
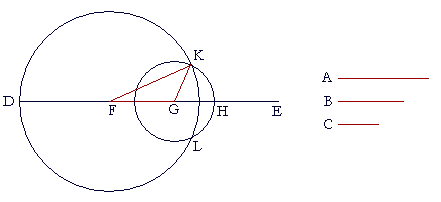 |
|
| Draw a straight line DE, which may be as long as we please in the | |
| direction of E; | (Postulate 2) |
| make DF equal to A, FG equal to B, and GH equal to C. | (I. 3) |
| With F as center and FD as radius, draw the circle DKL; | |
| with G as center and GH as radius, draw the circle HLK; | |
| and join KF and KG. | |
| Then we have constructed triangle KFG out of three straight lines equal to A, B, C. | |
| For, since the point F is the center of circle DKL, | |
| FD is equal to FK. | |
| But FD is equal to A; | (Construction) |
| therefore FK is equal to A. | |
 |
|
| Again, since the point G is the center of circle HLK, | |
| GH is equal to GK. | |
| But GH is equal to C; | |
| therefore GK is equal to C. | |
| And FG is equal to B. | |
| Therefore the three straight lines FK, FG, GK are equal to the three straight lines A, B, C. | |
| Therefore we have constructed the triangle KFG with sides KF, FG, GK equal to the three given straight lines A, B, C. Q.E.F. | |
![]()
In practice, it is not necessary to draw each entire circle, but only enough to determine the point K.
Note in this construction that the base of the triangle is the middle length B.
Duplication of an angle
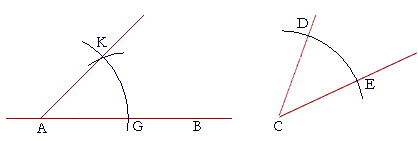
To duplicate angle DCE, for example, on a straight line AB at a point A on it, again, in practice it is necessary to determine only the point K.
With C as center and any radius CD, draw an arc DE.
With A as center and radius CD, draw an arc KG.
With G as center and radius ED, draw an arc that will intersect the first. That is the point K.
Draw KA. Then angle KAG will equal angle DCE.
(Before reading the proof below, do you see why?)
PROPOSITION 23. PROBLEM
| On a given straight line and at a given point on it, to construct an angle equal to a given angle. | |
| Let AB be the given straight line, A the given point on it, and DCE the given angle; | |
| we are required to construct on AB, and at the point A on it, an angle equal to angle DCE. | |
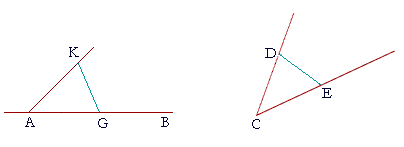 |
|
| On the straight line CD choose any point D; | |
| make CE equal to CD; | (I. 3) |
| and draw DE. | |
| Now construct triangle AGK in such a way that AG is equal to CE, | |
| AK is equal to CD, and KG is equal to DE. | (Proposition 22) |
| Then angle KAG will equal angle DCE. | |
| For, since the two sides KA, AG are equal to the two sides DC, CE respectively, | |
| and the base KG is equal to the base DE, | (Construction) |
| then angle KAG is equal to angle DCE. | (S.S.S.) |
| Therefore on the straight line AB and at A the given point on it, we have constructed an angle equal to the given angle DCE. Q.E.F. | |
![]()
This construction is not exactly Euclid's, but for practical purposes it is simpler. He did not make CE equal to CD, but chose D, E as any two points.
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com