11
APPLICATIONS
OF
MAXIMUM AND MINIMUM
VALUES
FINDING a maximum or a minimum (Lesson 10) has its application in pure mathematics, where for example we could find the largest rectangle that has a given perimeter. It also has its application to commercial problems, such as finding the least dimensions of a carton that is to contain a given volume.
Example 1. Find the dimensions of the rectangle that, for a given perimeter, will have the largest area.
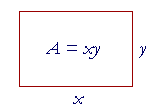
Solution. Let the base of the rectangle be x, let its height be y, let A be its area, and let P be the given perimeter. Then
P = 2x + 2y,
and
A = xy.
Since we are going to maximize A, we would like to have A as a function only of x. And we can do that because in the expression for P we can solve for y:
y = ½(P − 2x) = ½P − x.
Therefore,
| A | = | x(½P − x) | ||
| = | ½xP − x2. | |||
| On taking the derivative of A and setting it equal to 0, | ||||
| dA dx |
= | ½P − 2x | = | 0, |
| x | = | ¼P. | ||
The base is one quarter of the perimeter. We can now find the value of y:
y = ½P − ¼P = ¼P.
The height is also one quarter of the perimeter. That figure is a square![]() The rectangle that has the largest area for a given perimeter
The rectangle that has the largest area for a given perimeter
is a square.
(Note: The value we found is a maximum because the second derivative is negative.)
All maximum-minimum problems follow this same procedure:
| • | Write the function whose maximum or minimum value is to be determined. (In the Example, we wrote A = xy.) |
| • | The resulting expression will typically contain more than one variable. Use the information given in the problem to express every variable in terms of a single variable. (In the Example, we expressed y in terms of x.) |
| • | Find the critical value of that single variable by taking the derivative and setting it equal to 0. (In the Example, we took the derivative of A with respect to x.) |
| • | If necessary, determine the values of the other variables. (In the Example, we evaluated y by substituting the critical value of x.) |
In the following, notice how we follow these steps.
Example 2. A box having a square base and an open top is to contain 108 cubic feet. What should its dimensions be so that the material to make it will be a minimum? That is, what dimensions will cost the least?
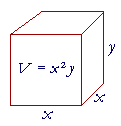
Solution. Let x be the side of the square base, and let y be its height. Then
| Area of base | = | x2. | |
| Area of four sides | = | 4xy. | |
| Let M be the total amount of material. Then | |||
| M | = | x2 + 4xy. | |
Now, how shall we express y in terms of x?
We have not yet used the fact that the volume must be 108 cubic feet. The volume is equal to
x2y = 108.
Therefore,
| y | = | 108 x2 |
||||
| and therefore in the expression for M, | ||||||
| 4xy | = | 4x· | 108 x2 |
= | ||
| M | = | |||||
| = | ||||||
| This implies, on multiplying through by the denominator x2: | ||||||
| 2x3 − 432 | = | 0 | ||||
| x3 | = | 216 | ||||
| x | = | 6 feet. | ||||
| We can now evaluate y: | ||||||
| y | = | |||||
These are the dimensions that will cost the least.
Example 3. Find the dimensions of the rectangle with the most area that can be inscribed in a semi-circle of radius r. Show, in fact, that the area of that rectangle is r2.
Solution. First, it should be clear that there is a rectangle with the
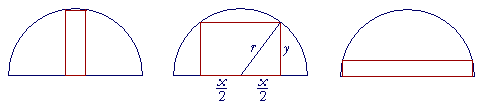
greatest area, as the figures above show.
Let x be the base of the rectangle, and let y be its height. Then, since r is the radius:
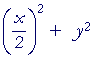 |
= | r2 | |
| = | r2 | ||
| x2 + 4y2 | = | 4r2. | |
| Therefore, | |||
| y | = | ||
Let A be the area we want to maximize. A = xy. That is,
| A | = | ||
| According to the product rule and the chain rule (Example 1): | |||
| dA dx |
= | 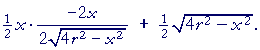 |
|
| −x2 + (4r2 −x2) | = | 0. | |
| This implies: | |||
| x2 | = | 2r2 | |
| x | = | ||
| This is the base of the largest rectangle. As for the height y: | |||
| y | = | ||
| y | = | ||
| y | = | ||
The area of this largest rectangle, then, is
![]()
Problem 1. Find two numbers whose sum is 42 and whose product will be the largest.
(Hint: Call the two numbers x and y. For convenience, call the product something. You will then have two equations in two unknowns. Express the product as function of a single variable, and find its maximum.)
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
The two numbers are 21 and 21.
Problem 2. You have a given length of fence. Using the wall of a house as one side of a rectangular fence, how would you place the fence around the other three sides in order to enclose the largest possible area?
Place half the fence parallel to the house.
Problem 3. Find the dimensions of the rectangle of maximum area that can be inscribed in a circle of radius r. Show, in fact, that that area will be 2r2.
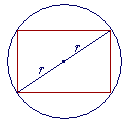
That figure is a square. Each side of the square is ![]() r.
r.
Problem 4. A can is to be constructed in the form of a right circular cylinder. If it is to contain a given volume V, what dimensions will require the least amount of material?
Show, in fact, that the height h of the can must equal its width, which is twice the radius r.
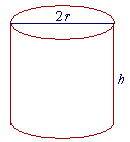
V = πr2h.
First, the top and bottom of the can are each a circle. And the area of the lateral surface is equivalent to a rectangle whose dimensions are 2πr × h. Therefore,
| The area A of the material | = | 2πr2 + 2πrh. |
From the formula for V, express h in terms of r.
| h | = |
V πr2 |
Therefore,
| A | = | 2πr2 + | 2V r |
| dA dr |
= | ||
A therefore has a minimum at
| r = | 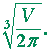 |
| h = | 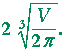 |
Compare Lesson 29 of Algebra, Problem 2.
The height of the can must equal its width, which is 2r.
Problem 5. Find the volume V of the largest right circular cone that can be inscribed in a sphere of radius r.
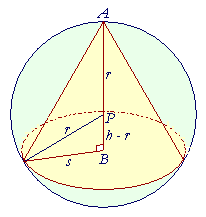
| V | = | 1 3 |
(area of the base)· (height). |
Let P be the center of the sphere of radius r. Let APB be the height of the cone, and call that height h. Then PB = h − r.
Let s be the radius of the cone. Then
| V = | 1 3 |
πs2h. |
We want to maximize V as a function of h alone. Therefore we must express s in terms of h and the constant r.
Now, s and h − r are the sides of a right triangle. Therefore,
| s2 + (h − r)2 | = | r2 |
| s2 + h2 − 2hr + r2 | = | r2 |
| s2 | = | 2hr − h2. |
| V | = | 1 3 |
π(2hr − h2)h. |
| = | π 3 |
(2h2r − h3). | |
| dV dh |
= | π 3 |
(4hr − 3h2). |
V therefore has a maximum at
| h | = | 4 3 |
r. |
Upon substituting that value for h in the expression for V above, that maximum volume is:
| V | = | 32 81 |
πr3. |
![]()
Next Lesson: Derivatives of trigonometric functions
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
