The meaning of a limit - An approach to calculus

An Approach

C A L C U L U S

LIMITS

under those vanishing conditions, requires the idea of a limit. And central to the idea of a limit is the idea of a sequence of rational numbers.

We encounter such a sequence in geometry when we determine a formula

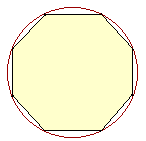for the area of a circle. To do that, we inscribe in the circle a regular polygon of n sides. The area of the polygon, which we can actually calculate, will be an approximation to the area of the circle. As we increase the number of sides -- that is, if we consider a sequence of polygons: 60 sides, 61 sides, 62, 63, 64, and so on -- then the sequence of those areas becomes closer and closer to the area of the circle. Now, the circle is never equal to a polygon. But by considering a sufficiently large number of sides, the difference between the circle and that polygon will be less than any small number we specify. Less, say, than

That is the idea of a sequence approaching a limit, or a boundary, which in this example is the area of the circle.

Problem 1. The student surely can recognize the number that is the limit of this sequence of rational numbers.

To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").

We speak of a sequence as being infinite, which, in analogy with the sequence of natural numbers, is a brief way of saying that, no matter how many terms, or which term, we name, there is a rule or a pattern that allows us to name one more.

Those values are getting closer and closer to 2 -- they are approaching 2 as their limit. 2 is the smallest number such that no matter which term of that sequence we name, it will be less than 2.

By "closer and closer" we mean the following. Choose an extremely small positive number. For example, "1 over the national debt

" Then we can name a term of that sequence such that the absolute value of the difference between that term and 2 will be less than that small number -- and the same will be true of any subsequent term that we name.

(We say the absolute value because the terms are less than 2, and so the difference itself will be negative.)

When a variable x approaches a number l as a limit, we symbolize that as x

l. Read: "The values of x approach l as a limit," or simply, "x approaches l." In the example above, x

2. "x approaches 2."

We also say that a sequence converges to a limit. The sequence above converges to 2.

By a sequence in what follows, we mean an ordering of rational numbers according to a rule or an indicated pattern. Here, for example, is a sequence that approaches 0:

Now the sequence we chose were values less than 2. And so we say that x approaches 2 from the left. We write

But we can easily construct a sequence of values of x that converges to 2 from the right; that is, a sequence of values that are more than 2.
For example,

But again, no matter what small number we specify, if we go far enough out in that sequence, the value of a difference |x − 2| will be less than that small number. And so will all subsequent differences we might name.

Again, when we say that the values of x "approach a limit," that limit is never a value of x. There is always a difference between the values of x and their limit. The limit is the boundary beyond which no member of the sequence will pass.

We summarize this in the following definition. But first, x is not the only variable. y is a variable. And y will be a function of x -- f(x) -- which is also a variable. And when we come to the definition of the derivative, Δx or h will be the variable. In the following, then, we will use the letter v to represent any variable.

DEFINITION 2.1. The limit of a variable. We say that a sequence of values of a variable v approaches a limit l (a number which is not a term in the sequence) if, beginning with a certain term v_n and any subsequent term we might name, the absolute value of v_n − l is less than any extremely small positive number that we specify.

When that condition is satisfied, we write v l.

Again, when a sequence approaches a limit, there is always a difference between the limit and the terms of the sequence. But the difference becomes less than the extremely small number required by the definition. The difference becomes practically zero. That is the essence of a variable approaching a limit.

If Δx is the variable that approaches the limit 0 (as it does when we determine the derivative), then Δx is never equal to 0.

We have defined the limit of a variable, but what we often have is a function of a variable -- which is also a variable. For example,

Now, a sequence of values of x will cause a sequence of values of f(x). The question is: Will those values of f(x) approach a limit L as the values of x approach a limit c ? If that is the case, then we write

In fact, let us see what happens to f(x) = x² as x

2−. Suppose again that x assumes this sequence of values:

The definition of the limit of a variable will be satisfied. f(x) = x² will approach 4 as a limit as x approaches 2.

And that sequence will also approach 4. Therefore 4 is the limit of x² whether x approaches 2 from the right or from the left. And so we can drop the + or − signs and simply write:

DEFINITION 2.2. The limit of a function. We say that a function
f(x) approaches a limit L as x approaches c if the sequence of values of x, both from the left and from the right, causes the sequence of values of f(x) to satisfy the definition of "approaches a limit L": Definition 2.1.

If that is the case, then we write:

"The limit of f(x) as x approaches c is L."

Thus for the limit of a function to exist as the independent variable approaches c , the left-hand and right-hand limits must be equal.

if and only if

When we say, then, that a function approaches a limit, we mean that Definition 2.2 has been satisfied. The theorems on limits imply that.

The most important limit -- the limit that differential calculus is about -- is called the derivative. All the other limits studied in Calculus I are logical fun and games, never to be heard from again.

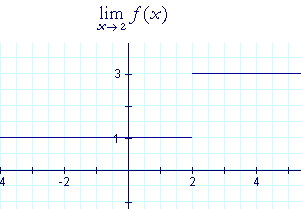
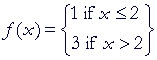
As x approaches 2 from the left, f(x) approaches 1. As x approaches 2 from the right, f(x) approaches 3. The left- and right-hand limits are not equal. Therefore, f(x) does not approach any limit as x approaches 2. Definition 2.2,