4
INTRODUCTION TO GRAPHS
The coördinate pairs of a function
WE WILL BEGIN with some basic vocabulary.
First, a coördinate. A coördinate is a number. It labels a point on a line.
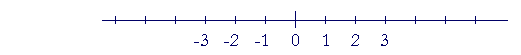
The coördinates 0, 1, 2, 3, etc. label those points. They are their "addresses."
A coördinate axis is a line with coördinates.
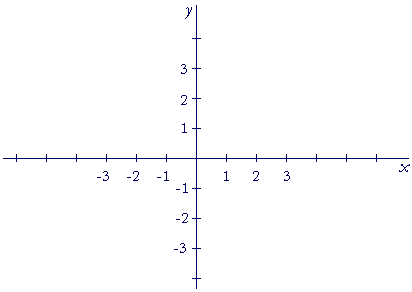
To label the points in a plane, we will need more than one coördinate axis, and we place them at right angles. Hence, they are called rectangular coördinate axes. And the coördinates on them are called rectangular coördinates. They are also called Cartesian coördinates, after the 17th century philosopher and mathematician René Descartes; for he was one of the first to exploit the geometrical possibilities of coördinates.
Finally, the rectangular coördinates of a point are an ordered pair, (x, y). (2, 3) labels a point different from (3, 2). The x-coördinate is always entered first; the y-coördinate, second.
Example 1. The graph of a function.
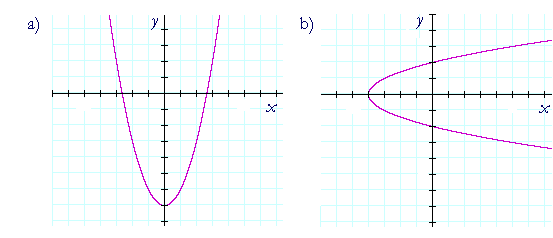
In which graph are the values of y a function of the values of x?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
In graph a). To each value of x there is one and only one value of y. Any straight line parallel to the y-axis will cut that graph only once.
The coördinate pairs of a function
Consider the function y = x2. The variable y now signifies the y-coördinate, and x, the x-coördinate. Therefore, every coördinate pair on the graph of that function is
(x, y) = (x, x2).
The y-coördinate is x2.
In other words, the graph of a function
y = f(x)
is that geometrical figure such that every coördinate pair on it is
(x, f(x)).
The y-coördinate is f(x).
For example, if
y = f(x) = x + 1,
then every coördinate pair on its graph has the form
(x, x + 1).
Problem 1. The coördinate pairs on the graph of the following functions have what form?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
| a) y = 1 − x | (x, 1 −x) | b) y = ax + b | (x, ax + b) | |
| c) y = 3 | (x, 3) | d) y = f(x) | (x, f(x)) | |
Problem 2. Let y = f(x). Write the second member of each coördinate pair.
| a) (1, ?) | (1, f(1)) | b) (−1, ?) | (−1, f(−1)) | |
| c) (a, ?) | (a, f(a)) | d) (t − 4, ?) | (t − 4, f(t − 4)) | |
Problem 3. Which of these points are on the graph of the function
y = 2x2 ?
| a) (1, 4) | No, because 4 is not equal to 2· 12. |
| b) (−1, 2) | Yes. | c) (a, 2a2) | Yes. | d) (b/2, b2/2) | Yes. |
Problem 4.
a) The coördinate pair (p, q) is on the graph of the function
f(x) = 3x + 7.
What is the relationship between the coördinates p, q?
q = f(p) = 3p + 7
b) The coördinate pair (r, s) is on the graph of the function
g(x) = 2x2 − 5x + 3.
What is the relationship between the coördinates r, s?
s = g(r) = 2r2 − 5r + 3
The height of the graph at x
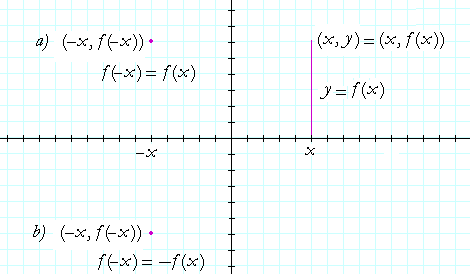
Let y = f(x). Then the coördinates of every point on its graph are
(x, f(x)). (Look at the first quadrant.)
f(x) -- or y -- is the height of the graph at x. It is the length of that vertical line.
Now, if f(−x) = f(x) -- that is, if the height of the graph at −x is equal to the height of the graph at x -- then that point is shown at a).
While if f(−x) = −f(x) -- if the height of the graph at −x is the negative of the height of the graph at x -- then that point is shown at b).
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
