12
Synthetic Division by x − a
IN ARITHMETIC we write, for example,
![]()
or,
| 47 5 |
= 9 + | 2 5 |
. |
Equivalently,
47 = 9· 5 + 2
5 is called the divisor, 47 is the dividend, 9 is the quotient, and 2 is the remainder.
| Dividend Divisor |
= Quotient + | Remainder Divisor |
Or,
Dividend = Quotient· Divisor + Remainder.
In algebra, if we divide a polynomial P(x) by a polynomial D(x) (where the degree of D is less than the degree of P), we would find
P(x) = Q(x)· D(x) + R(x).
P(x) is the dividend, Q(x) is the quotient, and R(x) is the remainder.
For example, if, by long division, we divided
x3 − 5x2 + 3 x − 7 by x − 2,
we would find
x − 2 |
= | x2 − 3x − 3 − | 13 x − 2 |
Or,
![]() = (x2 − 3x − 3)(x − 2) − 13.
= (x2 − 3x − 3)(x − 2) − 13.
x3 − 5x2 + 3x − 7 is the dividend, x2 − 3x −3 is the quotient, and −13 is the remainder.
Here is how to do this problem by synthetic division.
First, to use synthetic division, the divisor must be of the first degree and must have the form x − a. In this example, the divisor is x − 2, with a = 2.
Here again is the problem:
x − 2 |
Proceed as follows:
1. Write the coefficients of the dividend:
1 − 5 + 3 − 7
2. Put a, in this case 2, in a box to the right, leave a space, and draw a
2. line:
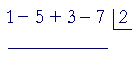
3. Bring down the leading coefficient (1), multiply it with a (2), and
3. write that product (1· 2) in the second column:
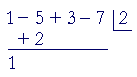
4. Add:
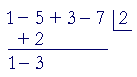
5. Repeat the process. −3· 2 = −6. And so on, until all the coefficients
5. have been exhausted.
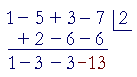
The first three numbers, 1 − 3 − 3, are the coefficients of the quotient, and the final number, −13, is the remainder.
We have
x3 − 5x2 + 3 x − 7 = (x2 − 3x −3)(x − 2) − 13.
Example 1. Use synthetic division to divide
2x5 + 3x4 + 25x2 − 1 by x + 3.
Solution. There are a couple of points here. First, we must account for all six coefficients of the general form.
2 + 3 + 0 + 25 + 0 − 1
The coefficient of x3 is 0, as is the coefficient of x.
Next, the divisor is x + 3. But the divisor must have the form x − a.
x + 3 = x − (−3).
Therefore, a = −3.
Here is the synthetic division:
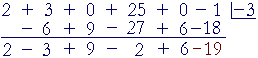
This tells us
x + 3 |
= | 2x4 − 3x3 + 9x2 − 2x + 6 − | 19 x + 3 |
Or,
| 2x5 + 3x4 + 25x2 − 1 | = | (2x4 − 3x3 + 9x2 − 2x + 6)(x + 3) − 19. |
| Dividend | = | Quotient· Divisor + Remainder. |
Note: The degree of the quotient is one less than the degree of the dividend. And the degree of the remainder is less than the degree of the divisor, x + 3, which in this case is 1. The remainder therefore is of degree 0, which is a number.
In general, if we divide a polynomial of degree n by a polynomial of degree 1, then the degree of the quotient will be n − 1. And the remainder will be a number.
Problem 1. Use synthetic division to divide
x3 − 8x2 + x + 2 by x − 7.
Write your answer in the form
P(x) = Q(x)· D(x) + R.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
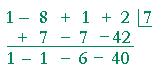
x3 − 8x2 + x + 2 = (x2 − x − 6)(x − 7) − 40
The remainder theorem
The value of a polynomial P(x) at x = a,
P(a),
is equal to the remainder upon dividing P(x)
by x − a.
That is, when
P(x) = Q(x)(x − a) + R,
where Q(x) is the quotient and R is the remainder, then
P(a) = R.
For,
| P(a) | = | Q(a)(a − a) + R |
| = | Q(a)· 0 + R | |
| = | 0 + R | |
| = | R. | |
Example 2. Let f(x) = x3 − 3x2 − 13x + 15.
We will use synthetic division to divide f(x) by x + 4.
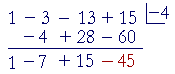
Now, what does the remainder theorem tell us?
The value of f(x) at x = −4, is equal to the remainder:
f(−4) = −45.
Now let us divide f(x) by x − 5:
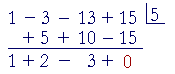
What does the remainder theorem tell us here?
f(5) = 0.
But this means that 5 is a root of f(x)![]()
Moreover, since the remainder is 0 -- there is no remainder -- then (x − 5) is a factor of f(x). The synthetic division shows:
x3 − 3x2 − 13x + 15 = (x2 + 2x − 3)(x − 5)
This illustrates the Factor Theorem:
The Factor Theorem. x − r is a factor of a polynomial P(x) if and only if r is a root of P(x).
Problem 2. Let f(x) = x3 − 5x2 − 4x + 7. Use synthetic division to divide f(x) by x − 7.
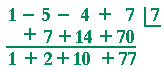
Therefore, according to the remainder theorem, f(7) = 77.
Since the remainder is not 0 -- f(7) ![]() 0 -- upon dividing f(x) by x − 7, then (x − 7) is not a factor of f(x). And according to the factor theorem, 7 is not a root of f(x).
0 -- upon dividing f(x) by x − 7, then (x − 7) is not a factor of f(x). And according to the factor theorem, 7 is not a root of f(x).
Problem 3. Let g(x) = 3x 4 + 17x3 + 16x 2 − 10x + 4. Use synthetic division to divide g(x) by x + 2.
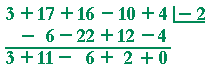
According to the remainder theorem, g(−2) = 0.
Therefore, what do you conclude about −2?
−2 is a root of g(x).
What do you conclude about (x + 2)?
(x + 2) is a factor of g(x).
Problem 4. Use synthetic division to divide
x3 + 125 by x + 5.
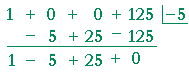
x3 + 125 = (x2 − 5x + 25)(x + 5)
Next Topic: Roots of polynomials
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
