3
ANGLES AND THEIR MEASUREMENT
WHEN TWO STRAIGHT LINES MEET they form an angle.
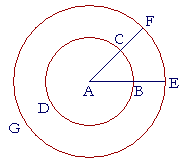
When the straight line FA meets the straight line EA, they form the angle we name as angle FAE. Letter A, which we place in the middle, labels the point where the two lines meet, and is called the vertex of the angle. When there is no confusion as to which point is the vertex, we may speak of "the angle at the point A," or simply "angle A."
The two straight lines that form an angle are called its sides. The size of the angle does not depend on the lengths of its sides. We can see that in the figure above. For if the point C is in the same straight line as FA, and B is in the same straight line as AE, then angles CAB and FAE are the same angle.
Now, to measure angle CAB, we place the vertex A at the center of a

circle; we call that a central angle. The sides CA, AB then intercept an arc BC. The measure of angle CAB will be the length of that arc -- relative to the length of the circumference. In degree measure, the circumference is 360 degrees. In what is called radian measure, we say it is 2π.
Those are the two systems for measuring angles.
Degree measure
To measure an angle in degrees, we imagine the circumference of a circle divided into 360 equal parts, and we call each of those equal parts a "degree." Its symbol is a small 0: 1° -- "1 degree." The full circle, then, will be 360°. But why the number 360? What is so special about it? Why not 100° or 1000°?
The answer is two-fold. First, 360 has many divisors, and therefore it will have many whole number parts. It has an exact half and an exact third -- which a power of 10 does not have. 360 has a fourth part, a fifth, a sixth, and so on. Those are natural divisions of the circle, and it is very convenient for their measures to be whole numbers. (Even the ancients didn't like fractions![]() )
)
Secondly, 360 is close to the number of days in the astronomical year: 365.
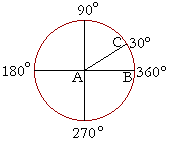
The measure of an angle, then, will be as many degrees as its sides intercept. To say that angle CAB is 30° means that its sides enclose 30 of those equal divisions. Arc BC is ![]() of the entire circumference.
of the entire circumference.
So, when 360° is the measure of a full circle, then 180° will be half a circle. 90° -- one right angle -- will be a quarter of a circle; and 270° will be three quarters of a circle: three right angles.
Let us now see how we deal with angles in the x-y plane.
Standard position
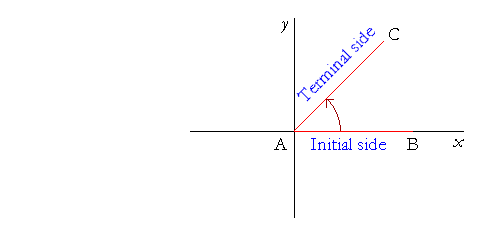
We say that an angle is in standard position when its vertex A is at the origin of the coördinate system, and its Initial side AB lies along the positive x-axis. We say that AB has "swept out" the angle BAC, and that AC is its Terminal side.
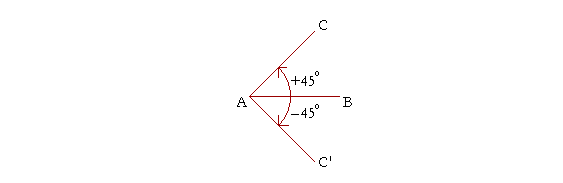
We now think of the terminal side AC as rotating about the fixed point A. When it rotates in a counter-clockwise direction, we say that the angle is positive. When it rotates in a clockwise direction, as AC', the angle is negative.
When the terminal side AC has rotated 360°, it has completed one full revolution.
Problem 1. How many degrees corresponds to each of the following?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
a) A third of a revolution A third of 360° = 120°
Lesson 15 of Arithmetic.
b) A sixth of a revolution A sixth of 360° = 60°
c) Five sixths of a revolution 5 × 60° = 300°
d) Two revolutions 2 × 360° = 720°
e) Three revolutions 3 × 360° = 1080°
f) One and a half revolutions 360° + 180° = 540°
Example 1. 30° is what fraction of a circle, or of one revolution?
| Answer. 30° is | 30 360 |
of a revolution: |
| 30 360 |
= | 3 36 |
= | 1 12 |
(Skill in Arithmetic, Equivalent Fractions, Question 5.)
Problem 2. What fraction of a revolution is each of the following?
| a) 60° | 60 360 |
= | 6 36 |
= | 1 6 |
| b) 45° | 45 360 |
= | 5 40 |
= | 1 8 |
| c) 72° | 72 360 |
= | 8 40 |
= | 1 5 |
Example 2. If the diameter of a circle is 16 cm, how long is the arc intercepted by a central angle of 45°?
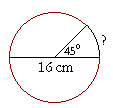
Answer. 45° is one eighth of a full circle. (It is half of 90 °, which is one quarter.) Now, the full circumference of this circle is
C = πD = 3.14 × 16 cm.
(Topic 2.) The intercepted arc is one eighth of the circumference:
3.14 × 16 ÷ 8 = 3.14 × 2 = 6.28 cm
Problem 3. If the diameter of a circle is 20 in, how long is the arc intercepted by a central angle of 72°?
We saw in Problem 2c) that 72° is one fifth of a circle. The circumference of this circle is C = πD = 3.14 × 20 in. The intercepted arc is one fifth of this: 3.14 × 20 ÷ 5 = 3.14 × 4 = 12.56 in.
The four quadrants
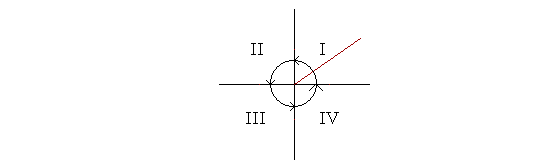
The x-y plane is divided into four quadrants. An angle begins in its standard position in the first quadrant ( I ). As the angle continues -- in the counter-clockwise direction -- we name each succeeding quadrant.
Why do we name the quadrants in the counter clockwise direction? Because in what we call the "first" quadrant, the algebraic signs of x and y are positive.
Problem 4. In which quadrant does each angle terminate?
a) 15° I b) −15° IV c) 135° II
d) 390° I. 390° = 360° + 30°
e) 100° II
f) −460° III. −460° = −360° − 100°
| g) 710° | IV. 710° is 10° less than two revolutions, which are 720°. |
Coterminal angles
Angles are coterminal if, when in the standard position, they have the same terminal side.
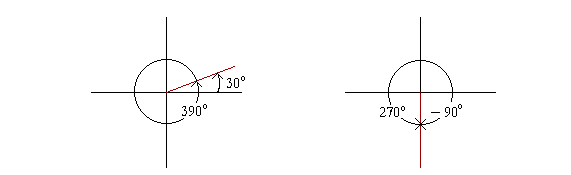
For example, 30° is coterminal with 360° + 30° = 390°. They have the same terminal side. That is, their terminal sides are indistinguishable.
Any angle θ is coterminal with θ + 360° -- because we are just going around the circle one complete time.
−90° is coterminal with 270°. Again, they have the same terminal side.
Note: 90° plus 270° = 360°. The sum of the absolute values of those coterminal angles completes the circle.
Problem 5. Name the non-negative angle that is coterminal with each of these, and is less than 360°.
a) 360° 0°
b) 450° 90°. 450° = 360° + 90°
c) −20° 340°
d) −180° +180°
e) −270° 90°
f) 720° 0°. 720° = 2 × 360°
| g) −200° | 160° |
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com