Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

THE THREE ANGLES OF A TRIANGLE
Book I. Propositions 31 and 32
THE NEXT TWO PROPOSITIONS depend on the fundamental theorems of parallel lines: Propostion 27 and its converse, Proposition 29.
Here again is
Proposition 29. If two straight lines are parallel, then a straight line that meets them makes the alternate angles equal, it makes the exterior angle equal to the opposite interior angle on the same side, and it makes the interior angles on the same side equal to two right angles.
Whenever we know that two straight lines are parallel, those are the conclusions that we can draw.
We will now present the well-known theorem about the three angles of a triangle, which is that they are equal to two right angles. But first, we must solve the following problem.
PROPOSITION 31. PROBLEM
| Through a given point to draw a straight line parallel to a given straight line. | |
| Let A be the given point, and BC the given straight line; we are required to draw a straight line through the point A parallel to BC. |
|
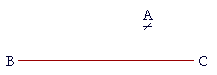 |
The construction and proof are straightforward, and they are left as an exercise. (Problem 1)
We are now ready to prove that the three angles of a triangle are together equal to two right angles.
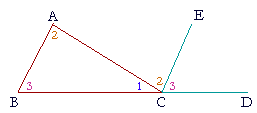
For, on extending BC to D, and drawing CE parallel to BA, the angles BAC, ACE labeled 2 are alternate angles; angle 3 on the right is exterior to the parallel lines and is equal to the interior angle 3. Angles 1, 2, 3 whose common vertex is at C will be proved equal to two right angles. And they are equal to angles 1, 2, 3 of the triangle.
Here is the formal proposition.
PROPOSITION 32. THEOREM
| If one side of a triangle is extended, then the exterior angle is equal to the two opposite interior angles; and the three interior angles of a triangle are equal to two right angles. | |
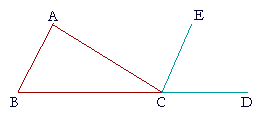
| Let ABC be a triangle, with side BC extended to D. Then the exterior angle ACD is equal to the two interior and opposite angles CAB, ABC; and the three interior angles ABC, BCA, CAB are together equal to two right angles. |
|
 |
|
| Through the point C draw CE parallel to AB. | (I. 31) |
| Then, since AB is parallel to CE, and AC meets them, | |
| the alternate angles BAC, ACE are equal. | (I. 29) |
| Also, since AB is parallel to CE and BD meets them, | |
| angle ECD, which is exterior to those parallels, is equal to the opposite interior angle ABC; | (I. 29) |
| and we proved that angle ACE was equal to angle BAC; | |
| therefore the whole exterior angle ACD is equal to the two interior angles CAB, ABC. |
(Axiom 2) |
| To each of these equals join angle ACB; | |
| therefore angles ACD, ACB are equal to the three angles CBA, BAC, ACB. |
(Axiom 2) |
| But angles ACD, ACB are equal to two right angles; | (I. 13) |
| therefore the three angles CBA, BAC, ACB are together also equal to two right angles. | (Axiom 1) |
| Therefore, if a side of a triangle etc. Q.E.D. | |
Corollary. The interior angles of any polygon are together equal to twice as many right angles as the figure has sides, less four right angles.
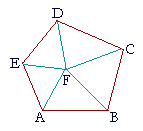
For, we can divide any polygon ABCDE into as many triangles as the figure has sides, by drawing straight lines from any point F within the figure to each vertex.
Now, all the angles of those triangles are equal to twice as many right angles as there are triangles, that is, as the figure has sides.
And those angles are all the interior angles of the figure, together with all the angles at the point F,
which are equal to four right angles. (I. 13. Corollary 2.)
Therefore all the interior angles of any polygon are equal to twice as many right angles as the figure has sides, less four right angles.
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com