Book I. Propositions 27 and 28
Problems
Back to Proposition 27.
1. In this figure:
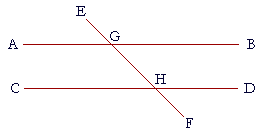
1. a) Name the two pairs of alternate angles.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
Angles AGH, GHD, and angles BGH, GHC.
1. b) Name the interior angles on the same side.
Angles AGH, GHC, and angles BGH, GHD.
1. c) Name the exterior angles on the same side.
Angles EGA, CHF, and angles EGB, FHD.

1. d) Name the angle which is on the same side and interior and
1. d) opposite to angle EGB; GHD;
1. d)
to angle EGA; GHC;
1. d)
to angle FHD; HGB.
2. When a straight line meets two straight lines, why is each pair of
2. alternate interior angles equal respectively to a pair of alternate
2. exterior angles? (Hence we may speak simply of the alternate
2. angles.)
Because they are vertical angles.
3. State the definition of parallel lines.
Parallel lines are straight lines that are in the same plane and do not meet, no matter how far extended in either direction.
4. a) State the hypothesis of Proposition 27.
A straight line that meets two straight lines makes the alternate angles equal.
2. b) State the conclusion.
The two straight lines are parallel.
2. c) Practice Proposition 27.
5. a) State the converse of Proposition 27.
If two straight lines are parallel, then a straight line that meets them makes the alternate angles equal.
(Do you think it's true?) It will be Proposition 29.
5. b) State the inverse of Proposition 27.
If a straight line that meets two parallel straight lines does not make the alternate angles equal, then the two straight lines are not parallel.
5. c) State its contrapositive.
If two straight lines are not parallel, then a straight line that meets them does not make the alternate angles equal.
5. d) Of those four propositions -- Proposition 27, its converse,
5. d) inverse, and contrapositive -- which ones are logically equivalent?
Proposition 27 and its contrapositive. The converse and the inverse. (See the Introduction to Logic.)
6. a) State the hypothesis of Proposition 28.
A straight line that meets two straight lines makes an exterior angle equal to the opposite interior angle on the same side, or it makes the interior angles on the same side equal to two right angles.
6. b) State the conclusion.
The two straight lines are parallel.
6. c) Practice Proposition 28.
7. a) State the converse of the first hypothesis of Proposition 28.
If two straight lines are parallel, then a straight line that meets them makes an exterior angle equal to the opposite interior angle on the same side.
7. b) State the converse of the second hypothesis of Proposition 28.
If two straight lines are parallel, then a straight line that meets them makes the interior angles on the same side equal to two right angles.
7. c) State the inverse of the second hypothesis of Proposition 28.
If a straight line that meets two straight lines makes the interior angles on the same side less than or greater than two right angles, then the two straight lines are not parallel.
8. Name three ways of proving lines parallel.
The alternate angles are equal.
An exterior angle is equal to the opposite interior angle on the same side.
The interior angles on the same side are equal to two right angles.
Table of Contents | Introduction | Home
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com