![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

I N T R O D U C T I O N
Geometry: The Study of Figures
IN THESE PAGES we present an English version of the very first textbook on geometry, a book assembled by the Greek scholar Euclid in the 4th century B.C.: the Elements of geometry and arithmetic. It is the most remarkable textbook the world has ever seen. Written in simple, straightforward language, the Elements has been translated the world over and through the centuries it has been the model for clear and eloquent reasoning. It was the first work to introduce what is called rigor into mathematics. That same rigor ("What gives us the right to say that we know?") is part of the culture of mathematics today, and it is the model followed by theoretical physics. Anyone truly interested in what mathematics is, can have no firmer foundation than Euclid.
Effort has always been made to express the Elements in the language of each time and place. The pages that follow are adapted from the translation by Sir Thomas Heath (Dover) as well as the edition of Isaac Todhunter (Elibron Classics).
What distinguishes Euclid's text from today's, is that it is completely verbal. There is no algebra, no symbols for "angle" or "equals." And there are no two-column proofs! Geometry in this way embraces logic, grammar and rhetoric, which were the classical liberal arts. What students see, they put into words. For geometry is based on looking; and the sensitivity it develops is the essence of science.
Now, we can see that when two sides of a triangle are equal, then the
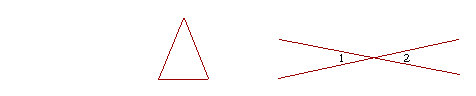
angles at the base are also equal. Or, when two straight lines meet, the angles labeled 1 and 2 are equal. But what distinguished the Greeks is that they wanted to explain why that was true. They were the first to present those facts in the framework of a logical science. And after introducing some terms, we will see precisely what that means.
Plane geometry
Geometry, which literally means land measurement, is the study of figures.
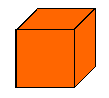
Let us begin with what we could actually experience, namely a cube. A cube is an example of a solid figure. Each of its boundaries, or faces, is the plane figure called a square. The boundaries of a square are straight lines. And the boundary, or end, of a line we call a point.

In this subject, we aspire to knowledge of plane figures: squares, circles, triangles. We want to know their properties and how to construct them. Plane geometry begins with the idea of each figure already in mind.
A line, which may be curved or straight, is a length. We do not mean length as opposed to width; we mean any actual or potential boundary of a plane figure. In the ultimate theorems, lines appear only as the boundaries of figures.
A line is length with no width. That is the idea of a line. What we draw, of course, has width and is a representation or a symbol for that idea, in the same way that a word is a symbol for the thing to which it refers. The word cat is not a cat. All communication is by means of symbols to evoke an idea.
A line may have boundaries, or extremities, and we call them points. A point is the idea of position only. It is the actual or potential end of a line.
We name a line by naming its endpoints with capital letters; thus we
![]()
speak of the line AB. Or we could call it BA, it does not matter, except if we want to emphasize that it extends in one direction, we would call it AB; if in the other direction, BA.
The space enclosed by the boundary—the figure itself—

is called area.
An angle is formed when two straight lines meet. The point—
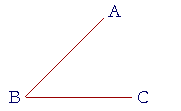
the place—where they meet is called the vertex of the angle. We name an angle with three letters—"angle ABC"—and we place the vertex in the center. When there is no doubt as to which point is the vertex, we may say "the angle at B," or simply "angle B."
Magnitudes
A magnitude is whatever has size: it could be larger or smaller. Length, area, and angle are the three kinds of magnitude we study in plane geometry. We compare magnitudes of the same kind, and we try to decide how they are related. Two lengths, two areas, or two angles either will be equal to one another, or one of them will be larger.
If we say, then, that these two triangles are equal—
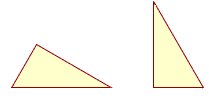
—we mean that they are equal areas. Because that is the kind of magnitude a triangle is. The space enclosed by each boundary will be exactly the same.
A magnitude is not like a natural number, because a magnitude is continuous, while a natural number, which is a collection of indivisible units, is discrete.
In algebra and arithmetic, the words length and area are often used to mean the measure of those magnitudes—a number. But in plane geometry, length and area are the magnitudes themselves, not numbers.
Straight lines
Each straight line that forms the boundary of a square,
![]() for example, will have two extremities; obviously. But we imagine that we could extend a straight line for as far as we please, and therefore we say that a straight line is potentially infinite. To be potentially infinite is in marked contrast to being actually infinite—which would mean that the straight line has no endpoints at all.
for example, will have two extremities; obviously. But we imagine that we could extend a straight line for as far as we please, and therefore we say that a straight line is potentially infinite. To be potentially infinite is in marked contrast to being actually infinite—which would mean that the straight line has no endpoints at all.
It is important to keep in mind that a line is the idea of length only. That idea will exist. But we will see that a line will have its mathematical existence when we have drawn it and thus are able to perceive it. And we draw a line to be the boundary of a figure. Therefore we have no need even for the idea of an actually infinite line. In what is called analytic geometry, however, they say they do need such lines. But in plane geometry, we require only the actual or potential boundary of a figure. Hence when we speak of a straight line in these pages, we mean what we can witness and draw: a line with two extremities.
This completes the preliminary description, this is what plane geometry is about; we are now ready to study it as a logical science.
Logic
The method of logic is to know something or to prove it through reasoning. Logic provides one answer to the question, "How do I know?" One can reply, "I deduced it." (Latin de, away from + ducere, to lead.) Hence when we deduce or prove something, we are led, through reasoning, from what we know to what we can conclude.
The statements we prove are called theorems. But it is not possible to prove every statement. If we had to, there would be no end. Rather, to prove or explain anything is to do so in terms of something simpler, something that we acknowledge and accept. They are called postulates and axioms.
Similarly, it is not possible to give a verbal definition of every word, because we must already understand the words in which a definition is framed. An example from arithmetic is the impossibility of defining one. (Try.) That does not mean that you do not understand one. An example from geometry is a definition of a straight line. Is there something we know better, or is more fundamental, on which a definition could be based? If there were, then that is where geometry would begin.
Logic, then, which is the science of reasoning, is not founded on reasoning. It is founded on irreducible understanding, on what we call first principles. They provide the basis for proving. The first principles of Euclid's geometry are in three categories:
1) Definitions
2) Postulates
3) Axioms or Common Notions
The statements found there will justify the statements we will make in proving the Theorems and Problems that follow.
Before presenting the first principles, let us become familiar with the vocabulary of logic.
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com