Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

EQUALITY OF NON-CONGRUENT FIGURES
Book I. Propositions 37 and 38
THE NEXT TWO PROPOSITIONS give conditions for non-congruent triangles to be equal. They follow from the fact that every triangle is half of a parallelogram.
PROPOSITION 37. THEOREM
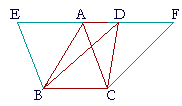
| Triangles on the same base and in the same parallels are equal. | |
| Let ABC, DBC be triangles on the same base BC and in the same parallels AD, BC; then triangle ABC is equal to triangle DBC. |
|
 |
|
| Extend AD in both directions to E and F; | |
| through B draw BE parallel to CA; | (I. 31) |
| and through C draw CF parallel to BD. | |
| Then each of the figures EBCA, DBCF is a parallelogram; | (Def. 15) |
| and they are equal | |
| because they are on the same base BC and in the same parallels BC, EF. | (I. 35) |
| But triangle ABC is half of the parallelogram EBCA because the diagonal AB bisects the parallelogram; | (I. 34) |
| And triangle DBC is half of the parallelogram DBCF because the diagonal DC bisects that parallelogram. | |
| And halves of equals are equal. | (Axiom 6) |
| Therefore triangle ABC is equal to triangle DBC. | |
| Therefore, triangles on the same base etc. Q.E.D. | |
![]()
Next:
PROPOSITION 38. THEOREM
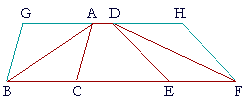
| Triangles on equal bases and in the same parallels are equal. | |
| Let ABC, DEF be triangles on equal bases BC, EF, and in the same parallels AD, BF; then triangle ABC is equal to triangle DEF. |
|
 |
|
| Extend AD in both directions to G and H; draw BG through B parallel to CA, and draw FH through F parallel to ED. |
(I. 31) |
| Then each of the figures GBCA, DEFH is a parallelogram; | (Def. 15) |
| and they are equal to one another because they are on equal bases BC, EF, and in the same parallels GH, BF. | (I. 36) |
| Moreover, triangle ABC is half of the parallelogram GBCA because the diagonal AB bisects it; |
(I. 34) |
| And triangle DEF is half of the parallelogram DEFH because the diagonal DF bisects it. |
|
| But halves of equals are equal. | (Axiom 6) |
| Therefore triangle ABC is equal to triangle DEF. | |
| Therefore, triangles on equal bases etc. Q.E.D. | |
![]()
These two propositions thus establish sufficient conditions for triangles to be equal. They must be on the same base or equal bases and in the same parallels, which is to say, they must have equal heights.
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com