Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

PARALLELOGRAMS
Book I. Propositions 33 and 34
WE ARE MAKING OUR final approach to the theorem of Pythagoras. But we first have to establish when figures that are not congruent will be equal. To do this, we will look at quadrilaterals whose opposite sides are parallel. Such a figure is called a parallelogram. (Definition 15.) The following proposition effectively shows that such a figure exists.
PROPOSITION 33. THEOREM
| The straight lines which join the extremities on the same side of two equal and parallel straight lines, are themselves equal and parallel. | |
| Let the straight lines AB, CD be equal and parallel, and let the straight lines AC, BD join their extremities that are on the same side; then AC, BD are themselves equal and parallel. |
|
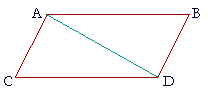 |
|
| Draw AD. | |
| Then, since AB is parallel to CD, | (Hypothesis) |
| and AD meets them, | |
| the alternate angles BAD, ADC are equal. | (I. 29) |
| And because AB is equal to CD, | |
| and AD is common to triangles ADB, ADC, | |
| the two sides BA, AD are equal to the two sides CD, DA respectively; | |
| and we showed that angle BAD is equal to angle ADC; | |
| therefore the remaining side AC is equal to the remaining side BD, | |
| and the remaining angles are equal to the remaining angles, namely those that are opposite the equal sides: | (S.A.S.) |
| angle CAD is equal to angle DBA. | |
| Therefore, since the straight line AD meets the two straight lines AC, BD and makes the alternate angles CAD, DBA equal, | |
| AC is parallel to BD. | (I. 27) |
| And we showed that they were equal. | |
| Therefore, if two straight lines etc. Q.E.D. | |
![]()
The proposition proves that if two sides of a quadrilateral are equal and parallel, then the figure is a parallelogram. (Definition 14.) Hence we may construct a parallelogram; for, Proposition 31 shows how to construct a straight line parallel to a given straight line.
The next theorem has for its hypothesis that a figure is a parallelogram, that is, the opposite sides are parallel. And it proves what is obvious to the eye: the opposite sides are equal.
This theorem will be fundamental to the theory of equal areas. In fact, as we have pointed out several times, when we say that two figures are "equal," we mean that they are equal areas. See Problems 1 and 2 following Proposition 4.
The student should look at the figure below and, given that the figure is a parallelogram, it should be clear why those two triangles are equal.
Why? S.A.S.
PROPOSITION 34. THEOREM
| In a parallelogram the opposite sides and angles are equal, and the diagonal bisects the area. | |
| Let ACDB be a parallelogram, and BC its diagonal; then the opposite sides and angles are equal, and the diagonal BC divides the parallelogram into two equal areas. |
|
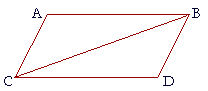 |
|
| Since AB is parallel to CD, and CB meets them, | |
| the alternate angles ABC, BCD are equal; | (I. 29) |
| and since AC is parallel to BD, and CB meeets them, | |
| the alternate angles ACB, CBD are equal. | |
| In triangles ABC, DCB, then, the two angles ABC, BCA are equal to the two angles DCB, CBD respectively, and the side BC is common; |
|
| therefore the remaining sides will equal the remaining sides: | |
| AB will equal CD, and AC will equal BD; | |
| and the remaining angle will equal the remaining angle: | |
| angle CAB will equal angle BDC. | (A.S.A.) |
| Also, because angle ABC is equal to angle BCD, | |
| and angle ACB is equal to angle CBD, | |
| the whole angle ABD is equal to the whole angle ACD. | (Axiom 2) |
| Therefore the opposite sides and angles of a parallelogram are equal. | |
 |
|
| Next, the diagonal bisects the parallelogram. | |
| For, since AB is equal to CD, and BC is common, | |
| the two sides AB, BC are equal to the two sides DC, CB respectively; | |
| and we have shown that angle ABC is equal to angle BCD; | |
| therefore triangles ABC, DCB are equal. | (S.A.S.) |
| Therefore the diagonal BC divides the parallelogram into two equal areas. | |
| Therefore, in a parallelogram etc. Q.E.D. | |
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com