Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

PERPENDICULARS
Book I. Propositions 11 and 12
WE ARE NOW GOING TO CONSTRUCT right angles. Not only will we show our geometrical skill, but we satisfy a requirement of logic: We will prove that these "right angles" that we have defined actually exist. For a definition is required only to be understood. We may not assume that what we have defined exists.
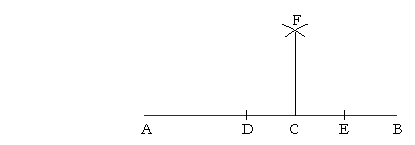
Thus, to draw a straight line at right angles to the straight line AB from the given point C, place the point of the compass at C, and mark off equal distances at D and E. With D as center and radius DE, draw an arc. With E as center and with the same radius, draw an arc, and call their point of intersection F. Then CF will be perpendicular to AB at C.
Do you see why?
Here is the proof.
PROPOSITION 11. PROBLEM
| To draw a straight line at right angles to a given straight line from a given point on it. | |
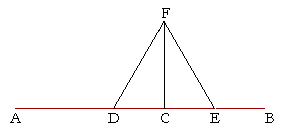
| Let AB be the given straight line, and C the given point on it; we are required to draw from the point C a straight line at right angles to the straight line AB. |
|
 |
|
| Choose any point D on AB; | |
| make CE equal to DC; | (I. 3) |
| on DE construct the equilateral triangle DFE; | (I. 1) |
| and draw CF. | |
| Then we have drawn the straight line CF at right angles to the given straight line AB, from C the given point on it. | |
| For, since DC is equal to CE, | (Construction) |
| and CF is common to triangles DCF, ECF, | |
| the two sides DC, CF are equal to the two sides EC, CF respectively; | |
| and the base DF is equal to the base EF; | (Construction) |
| therefore angle FCD is equal to angle FCE. | (S.S.S.) |
| And they are adjacent angles. | |
| And when a straight line that stands on another straight line makes the | |
| adjacent angles equal, each of those angles is a right angle; | (Definition 3) |
| therefore each of the angles FCD, FCE is a right angle. | |
| Therefore we have drawn CF at right angles to the given straight line AB, from C the given point on it. Q.E.F. | |
![]()
Using reductio ad absurdam we can prove:
Only one line can be drawn perpendicular to a given straight line
from a given point on it.
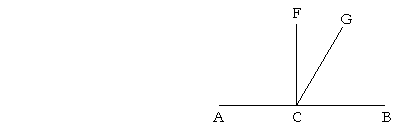
For if we suppose that CF and CG are both perpendicular to AB, then angle ACF is equal to angle ACG (Postulate 4),
the smaller to the larger; which is absurd.
Dropping a perpendicular
Propostion 12 is the problem of "dropping" a perpendicular:
To a given straight line that may be made as long as we please,
and from a given point not on it, to draw a perpendicular line.

Can you solve this problem? Can you draw a perpendicular line from C to AB?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
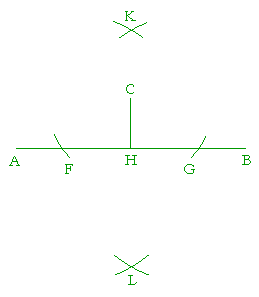
Place the point of the compass at C, and with a radius greater than the distance of C to AB, draw arcs at F and G. Now bisect the straight line FG at H. That is, with F as center and radius FG, draw arcs. With G as center and that same radius, draw arcs intersecting those at K and L. Then the straight line KCHL will be the perpendicular bisector of FG.
Why?
Here is the proof.
PROPOSITION 12. PROBLEM
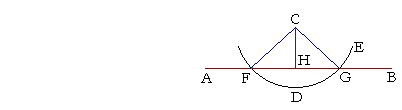
| To a given straight line that may be made as long as we please, and from a given point not on it, to draw a perpendicular line. | |
| Let AB be the given straight line, which we may extend to any length in either direction, and let C be the given point not on it; we are required to draw from the point C a straight line perpendicular to AB. |
|
 |
|
| Choose any point D on the other side of AB, and with C as center and CD as radius, draw the circle EDF, meeting |
|
| AB at F and G; | (Postulate 3) |
| bisect FG at H; | (I. 10) |
| and draw CH. | |
| Then the straight line CH will be perpendicular to the given straight line AB, from C the given point not on it. | |
| To prove that, draw CF and CG. | |
| Now, since FH is equal to HG, | (Construction) |
| and HC is common to the two triangles FHC, GHC, | |
| the two sides FH, HC are equal to the two sides GH, HC respectively; | |
| and the base CF is equal to the base CG; | (Definition 17 ) |
| therefore angle CHF is equal to angle CHG. | (S.S.S.) |
| And they are adjacent angles. | |
| And when a straight line that stands on another straight line makes the adjacent angles equal, each of those angles is a right angle, and the straight line that stands on the other is called a perpendicular to it. | |
| (Definition 3) | |
| Therefore we have drawn CH perpendicular to the given straight line AB, from C the given point not on it. Q.E.F. | |
This Proposition shows that it is possible to draw a line that satisfies the definition of a perpendicular line, and therefore what we have called a "perpendicular line" actually exists. (See the Commentary on the Definitions.)
The lines CF, CG are called auxiliary lines -- helping lines. They allow us to make triangles and hence compose the proof. The authority for drawing auxiliary lines is Postulate 1.
A word about what we mean by a given line or a given point, because those expressions occur in many propositions. For something to be given in this science, we must in some way be able to recognize it or know it. "That one." A line will be given if we can reproduce it.
For a point to be given, we must be able to reproduce its position. "There." This is analogous to the idea of a given number, which is a number we can recognize by its name; if it is not rational, then we must be able to approximate it by a rational number as closely as we please.
The requirement of given points, lines, and numbers insures that we do not lose touch with what we actually know.
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com