Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

THE ISOSCELES TRIANGLE
Book I. Proposition 5
EVEN THOUGH we practice the proofs of the theorems, they become hollow exercises unless we see that they are true. What we see becomes the proof -- there should be no gap between seeing and proving. Upon reading the enunciation, the setting out, and the specification of a theorem, the student should see that it is true. (Difficult to see might be the Pythagorean theorem, and perhaps that is why so many proofs have been offered.)
We are now ready to prove the well-known theorem about isosceles triangles, namely that the angles at the base are equal. And we can see that. Compare the isosceles triangle on the left
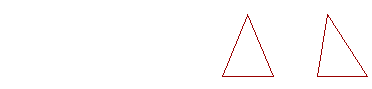
with the scalene triangle on the right.
There are several ways to prove this theorem, and we shall give the clever proof by Pappus, a Greek mathematician who followed Euclid in Alexandria. When we learn how to bisect an angle, we will see another proof. But this amusing proof is based clearly on what we see.
PROPOSITION 5. THEOREM
| In an isosceles triangle the angles at the base are equal. | |
| Let ABC be an isosceles triangle in which side AB is equal to side AC; | |
| then angle ABC is equal to angle ACB. | |
 |
|
| Let us conceive of this triangle as two triangles -- the triangles ABC | |
| and ACB -- and let us argue as follows. | |
| Since AB is equal to AC, and AC to AB, | (Hypothesis) |
| then the two sides BA, AC are equal to the two sides CA, AB respectively; | |
| and angle BAC is equal to angle CAB, because it is the same. | |
| Therefore those angles are equal that are opposite the equal sides: (S.A.S.) | |
| angle ABC, opposite side AC, is equal to angle ACB, opposite the equal side AB. | |
| Therefore, in an isosceles triangle the angles at the base are equal. | |
| Which is what we wanted to show. | |
Corollary. An equilateral triangle is equiangular.
![]()
A corollary is a proposition that follows from the previous proposition with little or no proof.
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com