14
DERIVATIVES OF LOGARITHMIC
AND
EXPONENTIAL FUNCTIONS
The derivative of e with a functional exponent
THE SYSTEM OF NATURAL LOGARITHMS has the number called e as it base; it is the system we use in all theoretical work. (In the next Lesson, we will see that e is approximately 2.718.) The system of natural logarithms is in contrast to the system of common logarithms, which has 10 as its base and is used for most practical work.
We denote the logarithmic function with base e as "ln x."
ln x = logex.
y = ln x implies e y = x.
In other words, this logarithm function --
y = ln x
-- has for its inverse the exponential function,
y = ex.
Here are the inverse relations:
ln ex = x and eln x = x.
And the logarithm of the base itself is always 1:
ln e = 1.
(Topic 20 of Precalculus.)
The function y = ln x is continuous and defined for all positive values of x. It will obey the usual laws of logarithms:
1. ln ab = ln a + ln b.
| 2. ln | a b |
= ln a − ln b. |
3. ln an = n ln a.
(Topic 20 of Precalculus.)
Like all the rules of algebra, they will obey the rule of symmetry.
For example,
n ln a = ln an.
The derivative of ln x
We will now apply the definition of the derivative to prove:
| d dx |
ln x | = | 1 x |
In the course of the proof, it will make for a great simplification if we define the base of the system of natural logs, the number we call e, as the following limit:
![]()
A limit in the proof will have that same form.
Later, we will call the variable x rather than v. And in the next lesson, upon changing the variable from v to ![]() , the familiar definition follows.
, the familiar definition follows.
Here is the difference quotient:
| according to the 2nd law; | |||
| = | 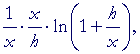 |
on multiplying by x/x; |
| = | 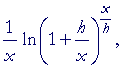 |
according to the 3rd law. |
We now take the limit as h approaches 0.
| = | 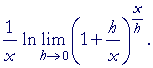 |
| The limit does not apply to | 1 x |
, because h is the variable |
| that is approaching 0. | 1 x |
is a constant factor. |
We now define that limit to be the base of the natural logarithms, the number we will call e. (That limit is the one above, with v = ![]() ; when
; when ![]() 0,
0, ![]()
![]() 0.)
0.)
Therefore,
| = | ||
| = | ||
| = | ||
Which is what we wanted to prove.
![]()
-- that is, e, exists as x approaches 0, here is the graph of
![]()
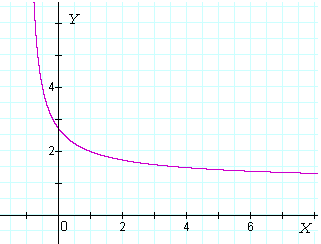
y has a definite value as x approaches 0. And in the next Lesson we will see that it is approximately 2.718.
The derivative of ex
We will now prove:
| d dx |
ex | = ex |
"The derivative of ex with respect to x
is equal to ex."
Since y = ex is the inverse of y = ln x, we can obtain its derivative as follows:
| y | = | ex | ||
| implies | ln y | = | ln ex | = x. |
Therefore on taking the derivative of both sides with respect to x, and applying the chain rule to ln y:
| = | 1. | ||
| y' | = | y. | |
| That is, | |||
| = | ex. | ||
ex is its own derivative.
What does that imply? It implies the meaning of exponential growth. For we say that a quantity grows "exponentially" when it grows at a rate that is proportional to its size. The bigger it is at any given time, the faster it's growing at that time. A typical example is population. The more individuals there are, the more births there will be, and hence the greater the rate of change of the population -- the number of births in each year.
All exponential functions have the form ax, where a is the base. Therefore, to say that the rate of growth is proportional to its size, is to say that the derivative of ax is proportional to ax.
| d dx |
ax | = kax | , |
where k is the constant of proportionality. (Lesson 39 of Algebra.) When we calculate that derivative below, we will see that that constant becomes ln a.
| d dx |
ax | = ln a· ax | . |
In the system of natural logarithms, in which e is the base, we have the simplest constant possible, namely 1.
| d dx |
ex | = ex. |
The derivative of e with a functional exponent
When y = eu(x), then according to the chain rule:
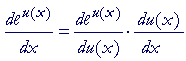
That is,
![]()
"The derivative of e with a functional exponent
is equal to e with that exponent
times the derivative of that exponent."
Example 1. Calculate the derivative of e2x + 3.
| Solution. |
Problem 1. Calculate the derivative of ex2.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
ex2· 2x = 2x ex2
Problem 2. Calculate the derivative of the following.
a) esin x. esin x cos x
b) e−x. e−x (−1) = −e−x
c) x2ex. x2ex + 2x ex
According to the product rule.
| d) | According to the quotient rule: |
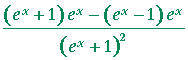 |
= | 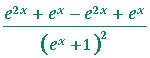 |
= | 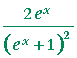 |
The derivative of ln u(x)
When y = ln u(x), then according to the chain rule:
![]()
That is,
![]()
| Example 2. |
| Example 3. | d dx |
ln sin x | = | 1 sin x |
· cos x | = | cos x sin x |
= cot x. |
Example 4. Find the derivative of ln x2.
Solution. We may apply the laws of logarithms:
| d dx |
ln x2 | = | d dx |
2 ln x, 3rd law, | |||
| = | 2 | d dx |
ln x | ||||
| = | 2 x |
. | |||||
| Example 5. Find the derivative of ln | x 3x − 4 |
. |
Solution. According to the 2nd Law:
| d dx |
ln | x 3x − 4 |
= | d dx |
[ln x − ln (3x − 4)] |
| = | |||||
| = | 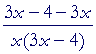 |
||||
| = | 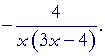 |
||||
Problem 3. Differentiate the following.
| a) ln x3. | d dx |
ln x3 = | d dx |
3 ln x | = | 3 x |
| b) (ln x)3. | 3(ln x)2· | 1 x |
= | 3(ln x)2 x |
| c) ln (3x2 − 4x). | 1 3x2 − 4x |
· (6x − 4) | = | 6x − 4 3x2 − 4x |
| d) ln (3x − 4)2. | 1 (3x − 4)2 |
· 2(3x − 4)· 3 | = | 6(3x − 4) (3x − 4)2 |
= | 6 3x − 4 |
| e) ln cos x. | 1 cos x |
(−sin x) | = | − | sin x cos x |
= | −tan x |
| Problem 4. Calculate the derivative of ln | 2 x |
. |
| d dx |
ln | 2 x |
= | d dx |
(ln 2 − ln x) = 0 − | 1 x |
= − | 1 x |
Problem 5. The derivative of logax.
According to the rule for changing from base e to a different base a:
![]()
![]()
![]()
Calculate the limit of that derivative
a) when x is greater than 1 and becomes larger.
That derivative approaches 0, that is, becomes smaller.
b) when x is less than 1 and becomes smaller.
That derivative becomes larger.
The general power rule
We can now prove that the derivative of f(x) = xn, where n is any rational exponent, is as follows:
| d dx |
xn | = nxn−1 |
Let
| y | = | xn. | ||
| Then | ||||
| ln y | = | n ln x (3rd Law). | ||
| Therefore, on taking the derivative with respect to x: | ||||
| = | n x |
|||
| so that | ||||
| y' | = | n x |
· y | |
| = | n x |
· xn | ||
| = | nxn−1. | |||
That is what we wanted to prove.
(If n is 0, then x0 = 1, a constant; its derivative is 0. If n is irrational, a rational approximation will be necessary.)
| Problem 6. Calculate the derivative of |
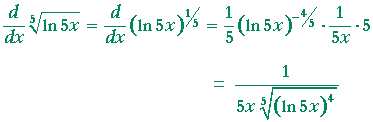
The derivative of ax
We will prove:
| d dx |
ax | = ln a· ax |
"The derivative of an exponential function with base a
is equal to the natural logarithm of that base
times the exponential function."
Let
| y | = | ax. | ||
| Then on taking the natural logarithm of both sides: | ||||
| ln y | = | x ln a. (3rd Law) | ||
| Therefore, | ||||
| = | ||||
| But by the chain rule: | ||||
| = | 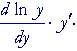 |
|||
| Therefore, | ||||
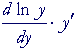 |
= | ln a. | ||
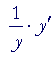 |
= | ln a | ||
| y' | = | ln a· y | ||
| That is, | ||||
| = | ln a· ax. | |||
This is what we wanted to prove.
| Example 6. | d dx |
2x | = ln 2· 2x. |
Problem 7. Calculate the derivative of y = 105x.
By the chain rule:
![]()
![]()
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
