9
LINEAR EQUATIONS
A logical sequence of statements
Transposing versus exchanging sides
AN EQUATION is an algebraic statement in which the verb is "equals" = . An equation involves an unknown number, typically called x. Here is a simple example:
x + 4 = 10.
"Some number, plus 4, equals 10."
We say that an equation has two sides: the left side, x + 4, and the right side, 10.
Because x appears to the first power, we call that a linear equation. A linear equation is also called an equation of the first degree.
The degree of any equation is the highest exponent that appears on the unknown number. An equation of the first degree is called linear because, as we will see much later, its graph is a straight line.
The equation -- that statement -- will become true only when the unknown has a certain value, which we call the solution to the equation.
The solution to that equation is obviously 6:
6 + 4 = 10.
6 is the only value of x for which the statement "x + 4 = 10" will be true. We say that x = 6 satisfies the equation.
Now, algebra depends on how things look. As far as how things look, then, we will know that we have solved an equation when we have isolated x on the left.
Why the left? Because that's how we read, from left to right. "x equals . . ."
In the standard form of a linear equation -- ax + b = 0 -- x appears on the left.
In fact, we have seen that, for any equation that looks like this:
| x + a | = | b, |
| the solution will always look like this: | ||
| x | = | b − a. |
| If | |||
| x + 4 | = | 10, | |
| then | |||
| x | = | 10 − 4 | |
| = | 6. | ||
The law of inverses
There are two pairs of inverse operations. Addition and subtraction, multiplication and division.
Formally, to solve an equation we must isolate the unknown on one side of the equation.
ax − b + c = d.
We must get a, b, c over to the other side, so that x is alone.
The question is:
How do we shift a number from one side of an equation
to the other?
Answer:
By writing it on the other side with the inverse operation.
That is the law of inverses. It follows from the two Rules of Lesson 5.
Example 1. Solve this equation:
| ax − b + c | = | d. |
| Solution. Since b is subtracted on the left, we will add it on the right: | ||
| ax + c | = | d + b. |
| Since c is added on the left, we will subtract it on the right: | ||
| ax | = | d + b − c. |
| And finally, since a multiplies on the left, we will divide it on the right: | ||
| x | = | d + b − c a |
We have solved the equation.
The four forms of equations
Solving any linear equation, then, will fall into four forms, corresponding to the four operations of arithmetic. The following are the basic rules for solving any linear equation. In each case, we will shift a to the other side.
1. If x + a = b, then x = b − a.
"If a number is added on one side of an equation,
we may subtract it on the other side."
2. If x − a = b, then x = b + a.
"If a number is subtracted on one side of an equation,
we may add it on the other side."
"If a number multiplies one side of an equation,
we may divide it on the other side."
| 4. If | x a |
= b, then x = ab. |
"If a number divides one side of an equation,
we may multiply it on the other side."
In every case, a was shifted to the other side by means of the inverse operation. It will be possible to solve any linear equation by applying one or more of those rules..
When the operations are addition or subtraction (Forms 1 and 2), we call that transposing.
We may shift a term to the other side of an equation
by changing its sign.
+ a goes to the other side as − a.
− a goes to the other side as + a.
Transposing is one of the most characteristic operations of algebra, and it is thought to be the meaning of the word algebra, which is of Arabic origin. (Arabic mathematicians learned algebra in India, from where they introduced it into Europe.) Transposing is the technique of those who actually use algebra in science and mathematics -- because it is skillful. And as we are about to see, it maintains the clear, logical sequence of statements. Moreover, it emphasizes that you do algebra with your eyes. When you see
| x + a | = | b, |
| then you immediately see that +a goes to the other side as −a: | ||
| x | = | b − a. |
What is often taught, though, is to actually write −a on both sides, draw a line and add.
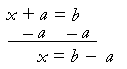
First, you will never see that in any calculus text. What you will see is a logical sequence of statements, which we are about to come to.
What is more, we proved that we may simply transpose. It is not necessary to prove it again every time you solve an equation.
(Do you have to prove the Pythagorean theorem every time you apply it? No, you do not.)
If you want to imagine that you have subtracted a from both sides, fine. But to have to write it is not skillful.
Here is what you will see in your calculus text.
A logical sequence of statements
Let us consider again the equation of Example 1.
ax − b + c = d.
That algebraic sentence -- that statement -- will logically imply other statements. We will now see the logical sequence that leads to the final statement, which is the solution.
| (1) | ax − b + c | = | d | |
| implies | (2) | ax | = | d + b − c |
| implies | (3) | x | = | d + b − c . a |
The original equation (1) is "transformed" by first transposing the terms. Statement (1) implies statement (2).
That statement is then transformed by dividing by a. Statement (2) implies statement (3), which is the solution.
Thus we solve an equation by transforming it -- changing how it looks -- statement by statement, line by line according to the rules of algebra, until x finally is isolated on the left. That is how books on mathematics are written (but unfortunately not books that teach algebra!). Each line is its own readable statement that follows from the line above -- with no crossings out.
In other words, What is a calculation? It is a discrete transformation of symbols. In arithmetic we transform "19 + 5" into "24". In algebra we transform "x + a = b" into "x = b − a."
Problem 1. Write the logical sequence of statements that will solve this equation for x :
abcx − d + e − f = 0
To see the answer, pass your mouse from left to right
over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| (1) | abcx − d + e − f | = | 0 | |
| implies | (2) | abcx | = | d − e + f |
| implies | (3) | x | = | d − e + f . abc |
First, transpose the terms. Line (2).
It is not necessary to write the term 0 on the right.
Then divide by the coefficient of x.
Problem 2. Write the logical sequence of statements that will solve this equation for x :
| (1) | 2x + 5 | = | 27 | |
| implies | (2) | 2x | = | 27 − 5 = 22 |
| implies | (3) | x | = | 22 2 |
| implies | (4) | x | = | 11. |
In Problems 3, 4, and 5, only the solution is given. The student should write the logical sequence of statements that leads to it.
Problem 3. Solve for x : (p − q)x + r = s
| x = | s − r p − q |
Problem 4. Solve for x :
ab(c + d)x − e + f = 0
| x = | e − f ab(c + d) |
Problem 5. Solve for x : 2x + 1= 0
x = −½
Each of the equations above are in the standard form, namely:
ax + b = 0.
a does not mean a. It means the coefficient of x. And b does not mean b. It means whatever the terms are.
That is why it is called a form. Whatever looks like that.
| Problem 6 . Solve: | ax + b | = | 0. | |
| x | = | − | b a |
|
This simple equation illustrates doing algebra with your eyes. The student should see the solution immediately. You should see that b will go to the other side as −b, and that a will divide.
That is skill in algebra.
Problem 7. Solve for x : ax = 0 (a![]() 0).
0).
Now, when the product of two numbers is 0, then at least one of them must be 0. (Lesson 6.) Therefore, any equation with that form has the solution,
x = 0.
We could solve that formally, of course, by dividing by a.
| x = | 0 a |
= 0. |
| (Lesson 6.) | ||
Problem 8. Solve for x :
| 4x − 2 | = | −2 |
| 4x | = | −2 + 2 = 0 |
| x | = | 0. |
Problem 9. Write the sequence of statements that will solve this equation:
| (1) | 6 − x | = | 9 |
| (2) | −x | = | 9 − 6 |
| (3) | −x | = | 3 |
| (4) | x | = | −3. |
When we go from line (1) to line (2), −x remains on the left. For, the terms in line (1) are 6 and −x.
We have "solved" the equation when we have isolated x -- not −x -- on the left. Therefore we go from line (3) to line (4) by changing the signs on both sides. (Lesson 5.)
Alternatively, we could have eliminated −x on the left by changing all the signs immediately:
| (1) | 6 − x | = | 9 |
| (2) | −6 + x | = | −9 |
| (3) | x | = | −9 + 6 = −3. |
| Problem 10. Solve for x : | 3 − x | = | −5 |
| x | = | 8. | |
Problem 11. Solve for x :
| 4 − (2x − 1) | = | −11. |
| 4 − 2x + 1 | = | −11. |
| 5 − 2x | = | −11 |
| −2x | = | −11 − 5 |
| 2x | = | 16 |
| x | = | 8. |
Problem 12. Solve for x:
| 3x − 15 2x + 1 |
= 0. |
(Hint: Compare Lesson 6, Problem 18.)
x = 5.
Transposing versus exchanging sides
| Example 2. | a + b = c − x |
We can easily solve this -- in one line -- simply by transposing x to the left, and what is on the left to the right:
x = c −a − b.
| Example 3. | a + b = c + x |
In this Example, +x is on the right. Since we want +x on the left, we can achieve that by exchanging sides:
c + x = a + b
Note: When we exchange sides, no signs change.
Upon transposing c, the solution easily follows:
c + x = a + b − c.
In summary, when −x is on the right, it is skillful simply to transpose it. But when +x is on the right, we may exchange the sides.
Problem 13. Solve for x :
| p + q | = | r − x − s | |
| Transpose: | |||
| x | = | r − s − p − q | |
Problem 14. Solve for x :
| p − q + r | = | s + x | |
| Exchange sides: | |||
| s + x | = | p − q + r | |
| x | = | p − q + r − s | |
Problem 15. Solve for x :
| 0 | = | px + q | |
| px + q | = | 0 | |
| px | = | − | q |
| x | = | − | q p |
Problem 16. Solve for x :
| −2 | = | −5x + 1 |
| 5x | = | 1 + 2 = 3 |
| x | = | 3 5 |
Problem 17. Solve for x :
| p | = | q −ax. |
| ax | = | q − p |
| x | = | q − p a |
Problem 18. Solve for cos θ ("cosine thay-ta").
| A | = | 8 − 2 cos θ. |
The thing to see is that this equation has exactly the same form as Problem 17. cos θ is the unknown. You will solve it exactly the same as Problem 17.
| 2 cos θ | = | 8 − A |
| cos θ | = | 8 − A 2 |
Algebra consists in recognizing the form. And there are only a finite number.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
