18
THE SQUARE OF A BINOMIAL
Perfect square trinomials
LET US BEGIN by learning about the square numbers. They are the numbers
1· 1 2· 2 3· 3
and so on. The following are the first ten square numbers -- and their roots.
| Square numbers | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
| Square roots | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1 is the square of 1. 4 is the square of 2. 9 is the square of 3. And so on.
The square root of 1 is 1. The square root of 4 is 2. The square root of 9 is 3. And so on.
In a multiplication table, the square numbers lie along the diagonal.
The square of a binomial
(x + 5)²
The square of a binomial come up so often that the student should be able to write the final product immediately. It will turn out to be a very specific trinomial. To see that, let us square the binomial (x + 5):
(x + 5)² = (x + 5)(x + 5) = x² + 10x + 25.
(See Lesson 16: Quadratic trinomials.)
x² + 10x + 25 is called a perfect square trinomial. It is the square of a binomial. To see what happens when we square any binomial, let us square (a + b):
(a + b)² = (a + b)(a + b) = a² + 2ab + b²
The square of any binomial produces the following three terms:
1. The square of the first term of the binomial: a²
2. Twice the product of the two terms: 2ab
3. The square of the second term: b²
The square of every binomial -- every perfect square trinomial -- has that form: a² + 2ab + b². To recognize that is to know an important product in the "multiplication table" of algebra.
(See Lesson 8 of Arithmetic: How to square a number mentally, particularly the square of 24, which is the "binomial" 20 + 4.)
Example 1. Square the binomial (x + 6).
Solution. (x + 6)² = x² + 12x + 36
x² is the square of x.
12x is twice the product of x· 6. (x· 6 = 6x. Twice that is 12x.)
36 is the square of 6.
Example 2. Square the binomial (3x − 4).
Solution. (3x − 4)² = 9x² − 24x + 16
9x² is the square of 3x.
−24x is twice the product of 3x· −4. (3x· −4 = −12x. Twice that is −24x.)
16 is the square of −4.
Note: If the binomial has a minus sign, then the minus sign appears only in the middle term of the trinomial. Therefore, using the double sign ± ("plus or minus"), we can state the rule as follows:
(a ± b)² = a² ± 2ab + b²
This means: If the binomial is a + b, then the middle term will be +2ab; but if the binomial is a − b, then the middle term will be −2ab
Example 3. (5x3 − 1)² = 25x6 − 10x3 + 1
25x6 is the square of 5x3. (Lesson 13: Exponents.)
−10x3 is twice the product of 5x3· −1. (5x3· −1 = −5x3. Twice that is −10x3.)
1 is the square of −1.
Example 4. Is this a perfect square trinomial: x² + 14x + 49 ?
Answer. Yes. It is the square of (x + 7).
x² is the square of x. 49 is the square of 7. And 14x is twice the product of x· 7.
In other words, x² + 14x + 49 could be factored as
x² + 14x + 49 = (x + 7)²
Note: If the coefficient of x had been any number but 14, this would not have been a perfect square trinomial.
Example 5 Is this a perfect square trinomial: x² + 50x + 100 ?
Answer. No, it is not. Although x² is the square of x, and 100 is the square of 10, 50x is not twice the product of x· 10. (Twice their product is 20x.)
Example 6 Is this a perfect square trinomial: x8 − 16x4 + 64 ?
Answer. Yes. It is the perfect square of x4 − 8.
Problem 1. Which numbers are the square numbers?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
1, 4, 9, 16, 25, 36, 49, 64, etc.
These are the numbers 1², 2², 3², and so on.
Problem 2.
a) State in words the formula for squaring a binomial.
The square of the first term.
Twice the product of the two terms.
The square of the second term.
b) Write only the trinomial product: (x + 8)² = x² + 16x + 64
c) Write only the trinomial product: (r + s)² = r² + 2rs + s²
Problem 3. Write only the trinomial product.
| a) | (x + 1)² = x² + 2x + 1 | b) (x − 1)² = | x² − 2x + 1 | |
| c) | (x + 2)² = x² + 4x + 4 | d) (x − 3)² = | x² − 6x + 9 | |
| e) | (x + 4)² = x² + 8x + 16 | f) (x − 5)² = | x² − 10x + 25 | |
| g) | (x + 6)² = x² + 12x + 36 | h) (x − y)² = | x² − 2xy + y² | |
Problem 4. Write only the trinomial product.
| a) | (2x + 1)² = 4x² + 4x + 1 | b) (3x − 2)² = | 9x² − 12x + 4 | |
| c) | (4x + 3)² = 16x² + 24x + 9 | d) (5x − 2)² = | 25x² − 20x + 4 | |
| e) | (x3 + 1)² = x6 + 2x3 + 1 | f) (x4 − 3)² = | x8 − 6x4 + 9 | |
| g) | (xn + 1)² = x2n + 2xn + 1 | h) (xn − 4)² = | x2n − 8xn + 16 | |
Problem 5. Factor: p² + 2pq + q².
p² + 2pq + q² = (p + q)²
The left-hand side is a perfect square trinomial.
Problem 6. Factor as a perfect square trinomial -- if possible.
| a) | x² − 4x + 4 = (x − 2)² | b) | x² + 6x + 9 = (x + 3)² | |
| c) | x² − 18x + 36 Not possible. | d) | x² − 12x + 36 = (x − 6)² | |
| e) | x² − 3x + 9 Not possible. | f) | x² + 10x + 25 = (x + 5)² | |
Problem 7. Factor as a perfect square trinomial, if possible.
| a) | 25x² + 30x + 9 = (5x + 3)² | b) | 4x² − 28x + 49 = (2x − 7)² | |
| c) | 25x² − 10x + 4 Not possible. | d) | 25x² − 20x + 4 = (5x − 2)² | |
| e) | 1 − 16y + 64y² = (1 − 8y )² | f) | 16m² − 40mn+ 25n² = (4m − 5n)² | |
| g) | x4 + 2x²y² + y4 = (x² + y²)² | h) | 4x6 − 10x3y4 + 25y8 Not possible. | |
Geometrical algebra
Here is a square whose side is a + b.
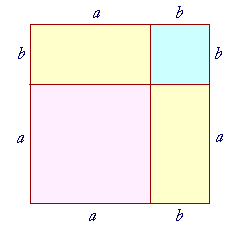
It is composed of
a square whose side is a,
a square whose side is b,
and two rectangles ab.
That is,
(a + b)² = a² + 2ab + b².
Next Lesson: The difference of two squares
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2010 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com