2
SIGNED NUMBERS
Positive and negative
The algebraic sign and the absolute value
Subtracting a larger number from a smaller
The algebraic definition of the negative of a number
IN ARITHMETIC we cannot subtract a larger number from a smaller.
2 − 3.
But in algebra we can. And to do it, we invent "negative" numbers.
2 − 3 = −1.
Now, to generate the positive numbers, we begin with 0 and successively add 1:
0, +1, +2, +3, +4, +5, and so on.
To generate the negative numbers, we begin with 0 and successively subtract 1:
0, −1, −2, −3, −4, −5, and so on.
We call all those numbers—positive, negative, and 0—the integers. We call those whole numbers integers to distinguish them from fractions and decimals. The positive integers are greater than 0. The negative integers are less. We call them both signed numbers.
1. What are the two parts of a signed number?
Its algebraic sign, + or − , and its absolute value, which is simply the arithmetical value, that is, the number without its sign.
The algebraic sign of +3 ("plus 3" or "positive 3") is + , and its absolute value is 3.
The algebraic sign of −3 ("negative 3" or "minus 3") is − . The absolute value of −3 is also 3.
The minus sign − is not only an algebraic sign. It is also the sign for the operation of subtraction. We will soon see how those two are related.
As for the algebraic sign + , normally we do not write it. The algebraic sign of 2, for example, is understood to be + .
As for 0, it is useful to say that it has both signs: −0 = +0 = 0.
(See
Lesson 5, Problem 9, and
Lesson 11, Problem 11.)
When we place a number within vertical lines, |−3|, that signifies its absolute value.
| |−3| | = | 3. |
| |3| | = | 3. |
Problem 1. Evaluate each of the following.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | |6| = 6 | b) | |−6| = 6 | c) | |0| = 0 | ||
| d) | |3 − 1| = 2 | e) | |1 − 3| = 2 | ||||
2. How do we subtract a larger number from a smaller?
5 − 8
1. What will be the sign of the answer?
It would not be wrong to say that we cannot take 8 from 5. We can of course take 5 from 8—and that is what we do—but we report the answer with a minus sign!
5 − 8 = −3.
Even in algebra we can only do ordinary arithmetic. But then we must choose the correct sign.
We may say that this is the first rule of signed numbers:
To subtract a larger number from a smaller,
subtract the smaller from the larger, but report
the answer as negative.
1 − 5 = −4.
We actually do 5 − 1.
It was in order to subtract a larger number from a smaller that negative numbers were invented.
Problem 2. What is the only difference between 8 − 5 and 5 − 8 ?
The algebraic signs. They have the same absolute value.
8 − 5 = 3. 5 − 8 = −3.
Problem 3. Subtract.
| a) 3 − 5 = −2 | b) 1 − 8 = −7 | |
| c) 8 − 14 = −6 | d) 20 − 65 = −45 | |
Problem 4. You have 20 dollars in the bank and you write a check for 25 dollars. Now what is your balance?
20.00 − 25.00 = −5.00
The number line
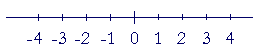
What you see above is called the number line. We imagine that it extends in both directions for as far as we please. The negative numbers fall to the left of 0. The positive numbers fall to the right.
When we draw the number line, we typically place the integers. However, every number we name will be on the number line. The fraction ½ will fall between 0 and 1; the fraction −½ is between 0 and −1; and so on.
It is on the number line in fact that we begin to see the practical uses for signed numbers. In general, they show the "direction" of some quantity. That quantity might be temperture: more than or less than a certain temperature designated as 0. Or it might be the position or "address" of some object: left or right of some fixed position chosen as 0. Or it might be the time: before or after a certain moment that again is chosen as 0. Or, as we all know, negative numbers can indicate a balance in a checking account![]()
Problem 5. A rocket is scheduled to launch at precisely 9:16 AM, which is designated t (for time) = 0, and t will be measured in minutes.
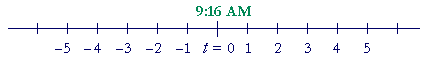
a) What time is it at t = −10? 9:06 AM.
b) What time is it at t = −1? 9:15 AM.
c) What time is it at t = +5? 9:21 AM.
d) What is the value of t at 9:00 AM? t = −16.
e) What is the value of t at 9:30 AM? t = 14.
The negative of any number
Every number will have a negative. The negative of 3, for example, will be found at the same distance from 0, but on the other side.
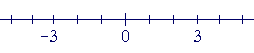
It is −3.
Now, what number is the negative of −3?
The negative of −3 will be the same distance from 0 on the other side. It is 3.
−(−3) = 3.
"The negative of −3 is 3."
This will be true for any number a:
−(−a) = a
"The negative of −a is a."
What is in the box is called a formal rule . This means that whenever we see something that looks like this --
−(−a)
-- something that has that form, then we may rewrite it in this form:
a
For example,
−(−12) = 12.
To learn algebra is to learn its formal rules. For what are calculations but writing things in a different form? In arithmetic, we rewrite 1 + 1 as 2. In algebra, we rewrite −(−a) as a.
See Lesson 5.
Problem 6. Evaluate the following.
a) −(−10) = 10 b) −(2 − 6) = 4
c) −(1 + 4 − 7) = 2 d) −(−x) = x
The algebraic definition of the negative of a number
Finally, the way we define a negative number in algebra is as follows. −5, for example, is that number which when added to 5 itself, results in 0.
5 + (−5) = 0.
That is, to each number a there corresponds one and only one number −a called its negative. And when we add it to a, we get 0.
a + (−a) = −a + a = 0
Problem 7. What number do you have to add to 8 in order to get 0?
−8
Problem 8. What number do you have to add to −6 in order to get 0?
6
Problem 9. What number is the negative of −q? Why?
The negative of −q is q, because −q + q = 0.
That is,
−(−q) = q.
Problem 10. If
s + t = 0,
then what is the relationship between t and s?
t = −s.
Problem 11. If you had to prove that
b − a is the negative of a − b,
how would you do it?
Show that a − b + b − a = 0 .
To prove a property of anything, whether in mathematics, logic or the law, we have simply to show that it satisfies the definition of that property.
Next Lesson: Adding and subtracting signed numbers
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
