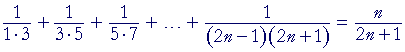27
MATHEMATICAL INDUCTION
The principle of mathematical induction
THE NATURAL NUMBERS are the counting numbers: 1, 2, 3, 4, etc. Mathematical induction is a technique for proving a statement -- a theorem, or a formula -- that is asserted about every natural number.
By "every", or "all," natural numbers, we mean any one that we name.
For example,
1 + 2 + 3 + . . . + n = ½n(n + 1).
This asserts that the sum of consecutive numbers from 1 to n is given by the formula on the right. We want to prove that this will be true for n = 1, n = 2, n = 3, and so on. Now we can test the formula for any given number, say n = 3:
1 + 2 + 3 = ½· 3· 4 = 6
-- which is true. It is also true for n = 4:
1 + 2 + 3 + 4 = ½· 4· 5 = 10.
But how are we to prove this rule for every value of n?
The method of proof is the following. We show that if the statement -- the rule -- is true for any specific number k (e.g. 104), then it will also be true for its successor, k + 1 (e.g. 105). We then show that the statement will be true for 1. It then follows that the statement will be true for 2. Therefore it will be true for 3. It will be true for any natural number we name.
This is called the principle of mathematical induction.
| If | ||
| 1) | when a statement is true for a natural number n = k, then it will also be true for its successor, n = k + 1; |
|
| and | ||
| 2) | the statement is true for n = 1; | |
| then the statement will be true for every natural number n. | ||
To prove a statement by induction, we must prove parts 1) and 2) above.
The hypothesis of Step 1) -- "The statement is true for n = k" -- is called the induction assumption, or the induction hypothesis. It is what we assume when we prove a theorem by induction.
Example 1. Prove that the sum of the first n natural numbers is given by this formula:
| 1 + 2 + 3 + . . . + n | = | n(n + 1) 2 |
. |
Proof. We will do Steps 1) and 2) above. First, we will assume that the formula is true for n = k; that is, we will assume:
| 1 + 2 + 3 + . . . + k | = | k(k + 1) 2 |
. (1) |
This is the induction assumption. Assuming this, we must prove that the formula is true for its successor, n = k + 1. That is, we must show:
| 1 + 2 + 3 + . . . + (k + 1) | = | (k + 1)(k + 2) 2 |
. (2) |
To do that, we will simply add the next term (k + 1) to both sides of the induction assumption, line (1):
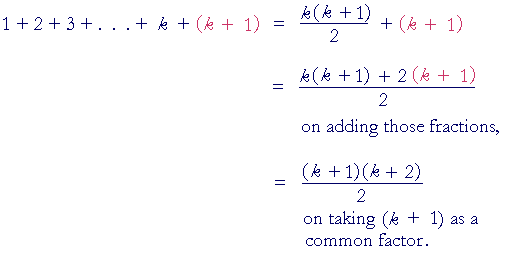
This is line (2), which is the first thing we wanted to show.
Next, we must show that the formula is true for n = 1. We have:
1 = ½· 1· 2
-- which is true. We have now fulfilled both conditions of the principle of mathematical induction. The formula is therefore true for every natural number.
(In the Appendix to Arithmetic, we establish that formula directly.)
Example 2. Prove that this rule of exponents is true for every natural number n:
(ab)n = anbn.
Proof. Again, we begin by assuming that it is true for n = k; that is, we assume:
(ab)k = akbk . . . . . . . . (3)
With this assumption, we must show that the rule is true for its successor, n = (k + 1). We must show:
(ab)k + 1 = ak + 1bk + 1. . . . . . . (4)
(When using mathematical induction, the student should always write exactly what is to be shown.)
Now, given the assumption, line (3), how can we produce line (4) from it ?
Simply by multiplying both sides of line (3) by ab:
| (ab)kab | = | akbkab | |
| = | akabkb | ||
| since the order of factors does not matter, | |||
| = | ak + 1bk + 1. | ||
This is line (4), which is what we wanted to show.
So, we have shown that if the theorem is true for any specific natural number k, then it is also true for its successor, k + 1.
Next, we must show that the rule is true for n = 1; that is, that
(ab)1 = a1b1.
But (ab)1 = ab; and a1b1 = ab.
This rule is therefore true for every natural number n.
Example 3. The sum of consecutive cubes. Prove this remarkable fact of arithmetic:
13 + 23 + 33 + . . . + n3 = (1 + 2 + 3 + . . . + n)2.
"The sum of n consecutive cubes is equal to the square
of the sum of the first n numbers."
In other words, according to Example 1:
| 13 + 23 + 33 + . . . + n3 | = | n²(n + 1)² 4 |
Proof. For convenience, we will denote the sum up to n by S(n). We assume, then, that the formula is true for n = k; that is, that
| S(k) | = | k²(k + 1)² 4 |
(1) |
| We must now show that the formula is also true for n = k + 1; that | |||
| S(k + 1) | = | (k + 1)²(k + 2)² 4 |
(2) |
| To do that, add the next cube to S(k), line (1): | |||
| S(k + 1) | = | S(k) + (k + 1)3 | |
| = | k²(k + 1)² 4 |
+ (k + 1)3 | |
| = | k²(k + 1)² + 4(k + 1)³ 4 |
||
| = | (k + 1)²[k² + 4(k + 1)] 4 |
||
| -- on taking (k + 1)2 as a common factor, | |||
| = | (k + 1)²(k² + 4k + 4) 4 |
||
| = | (k + 1)²(k + 2)² 4 |
||
This is line (2), which is what we wanted to show.
Finally, we must show that the formula is true for n = 1.
| 13 | = | 1²· 2² 4 |
| 1 | = | 1· 4 4 |
-- which is true. The formula therefore is true for every natural number.
In the Appendix to Arithmetic, we show directly that that is true.
Problem 1. According to the principle of mathematical induction, to prove a statement that is asserted about every natural number n, there are two things to prove.
a) What is the first?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
If the statement is true for n = k, then it will be true for its successor, k + 1.
b) What is the second?
The statement is true for n = 1.
c) Part a) contains the induction assumption. What is it?
The statement is true for n = k.
Problem 2. Let S(n) = 2n − 1. Evaluate
a) S(k) = 2k − 1
b) S(k + 1) = 2(k + 1) − 1 = 2k + 2 − 1 = 2k + 1
Problem 3. The sum of the first n odd numbers is equal to the nth square.
1 + 3 + 5 + 7 + . . . + (2n − 1) = n2.
a) To prove that by mathematical induction, what will be the induction
a) assumption?
The statement is true for n = k:
1 + 3 + 5 + 7 + . . . + (2k − 1) = k2.
b) On the basis of this assumption, what must we show?
The statement is true for its successor, k + 1:
1 + 3 + 5 + 7 + . . . + (2k − 1) + 2k + 1 = (k + 1)².
c) Show that.
On adding 2k + 1 to both sides of the induction assumption:
| 1 + 3 + 5 + 7 + . . . + (2k − 1) + 2k + 1 | = | k² + 2k + 1 |
| = | (k + 1)2 | |
d) To complete the proof by mathematical induction, what must we show?
The statement is true for n = 1.
e) Show that.
1 = 12
Problem 4. Prove by mathematical induction:
If we denote that sum by S(n), then assume that the formula is true for n = k; that is, assume
| S(k) | = | k 2k + 1 |
. |
Now show that the formula is true for n = k + 1; that is, show:
| S(k + 1) | = | k + 1 2k + 3 |
. |
Begin:
| S(k + 1) | = | S(k) + The next term, whose denominator is the product of the next odd numbers. |
| = | 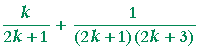 |
|
| = | 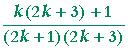 |
|
| = | 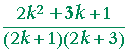 |
|
| = | 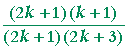 |
|
| = | ||
Next,
The formula is true for n = 1:
![]()
Therefore it is true for all natural numbers.
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com