11
INCOMMENSURABLE MAGNITUDES
The square drawn on the diagonal
HERE AGAIN IS THE THEOREM of the previous Lesson:
Two straight lines will have a common measure -- they will have the same ratio as two natural numbers -- if and only if the squares on them have the same ratio as two square numbers.
What, then, will be the case if two squares are not in the same ratio as two square numbers? What if one square is twice the size of another?
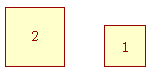
2 and 1 are not both square numbers. What must we say about the ratio of the sides?
The sides do not have the same ratio as two natural numbers. One side is not any multiple of the other, any part of it, or parts of it. Language is incapable of expressing how they are related.
Those sides do not have a common measure. We say that those sides are incommensurable.
Problem 1. If one square is three times the size of another square, then
a) are their sides commensurable or incommensurable?
a) (Commensurable means that they have a common measure.)
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Incommensurable. The squares are in the ratio 3 to 1, and 3 and 1 are not both square numbers.
b) if the side of one square is a multiple of one-eighth of an inch,
b) could the other side also be a multiple of one-eighth of an inch?
No. Those sides have no common measure.
c) if one side is so many millionths of an inch, could the other side
c) also be millionths of an inch?
No.
d) if one side is a multiple of any unit fraction, could the other side also
d) be a multiple of that unit fraction?
No.
e) Will those sides have the same ratio as two natural numbers? That
e) is, will one side be a multiple of the other, a part of it, or parts of it?
No.
f) If one side is a rational number of units, could the other side also be
f) a rational number of those units? Explain.
No. They cannot both be rational, because if they were, they would have a common measure. (Lesson 9.)
g) Can you express the ratio of those sides?
Can you?
Problem 2. How will we know when straight lines are incommensurable?
The squares on them are not in the same ratio as square numbers.
Problem 3.
a) If two squares are to one another as 9 is to 20, do their sides have a
a) common measure?
No. 9 and 20 are not both square numbers.
b) If two squares are to one another as 9 is to 25, do their sides have a
b) common measure?
Yes. What is the ratio of those sides; explicitly,
b) which multiple or part or parts of one is the other?
The smaller side is three fifths of the larger.
Problem 4. Let a square be 10 square meters.
a) Does that square have a common measure with 1 square meter?
Yes. 10 and 1 are natural numbers.
b) Will its side have a common measure with 1 meter?
No. 10 and 1 are not both square numbers.
c) Will its side be a rational number of meters?
No. The side has no common measure with 1 meter.
Problem 5.
a) If one square is four ninths of another square, is its side a fraction
a) of the other side?
Yes. 4 and 9 are square numbers.
b) If one square is four fifths of another square, is its side a fraction of
b) the other side?
No. 4 and 5 are not both square numbers.
Could both sides be a rational number of centimeters? No.
The square drawn on the diagonal
That two magnitudes could be incommensurable was realized by the Greek philosopher and mathematician Pythagoras, in the 6th century B.C. To see what Pythagoras saw, consider the square ABCD on the left:
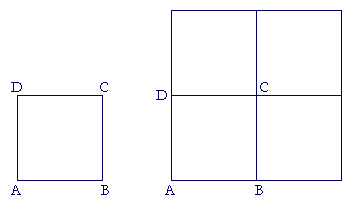
On the right, we have joined three equal squares, making a square four times as large.
Let us now cut each of those four equal squares in half:
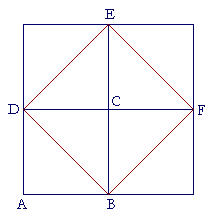
Then BFED is itself as square, and it is composed of four equal triangles. ABCD is composed of two of them. Therefore BFED is twice as large as ABCD.
Now, DB is called the diagonal of the square whose side is AB. We see:
The square drawn on the diagonal of a square
is twice the square on the side.
Problem 6. Are the diagonal DB and the side AB commensurable or incommensurable?
Incommensurable. The squares on them are in the ratio 2 : 1, and 2 is not a square number.

The student should know that this discovery -- The diagonal and side of a square are incommensurable -- was a landmark in the history of mathematics. It drove home the distinction between geometry and arithmetic; between what is continuous, namely length, and what is discrete: the names of the ratios of numbers. We are about to see that it led to the invention of what are now called irrational numbers.
Pythagoras realized that since the diagonal and side are not in the same ratio as two natural numbers, he could not say how they were related. He proved, in fact, that there is no number (that we now call rational) whose square is 2. He said that the relationship of the diagonal to the side was "without a name." That has been called mathematics first logical crisis.
Nevertheless, knowledge of a square figure is still rational: The square drawn on the diagonal is twice the square on the side. This suggests that the fundamental geometrical magnitude is not length but area. The figure itself.
Multiples that meet?
Consider two magnitudes of the same kind, a and b. Then if multiples

of them meet, that is, if a multiple of a is equal to a multiple of b, then those magnitudes are commensurable -- they have the same ratio as two natural numbers.
If four a's, for example, are equal to three b's, then that implies the ratio of a to b, namely a is three fourths of b. (Lesson 3.)
On the other hand, if a and b were incommensurable, then their
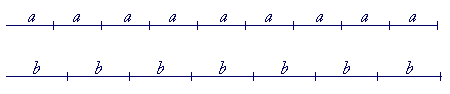
multiples would never meet, no matter how far they might be extended. Multiples of the diagonal and side of a square will never meet. A multiple of one will never be equal to a multiple of the other.
Problem 7. Since any two lengths could be measured with a ruler, and we always get a rational number, what sense does it make to say that two lengths are incommensurable?
Since lengths are continuous, with no units to count, we always have the problem of measuring exactly. Measurement is limited not only by the fineness of the measuring instrument, but also by the fineness of our eyes to see its readings. (Is it ![]() or 4
or 4![]() ?) Therefore, when we say that two lengths do, or do not, have a common measure, we mean as determined logically, not with rulers.
?) Therefore, when we say that two lengths do, or do not, have a common measure, we mean as determined logically, not with rulers.
Problem 8.
a) Again, what is the ratio that natural numbers have to one another?
One number is a multiple of the other, a part of it, or parts of it; or a mixture of those.
Express the following ratios:
| 5 to 1 | 5 is five times 1. | |
| 5 to 15 | 5 is the third part of 15. | |
| 5 to 8 | 5 is five eighths of 8. | |
| 5 to 2 | 5 is two and a half times 2 | |
b) Are magnitudes necessarily in the same ratio as natural numbers?
No. We cannot always express their relationship in words.
c) Therefore, what do we mean by the "ratio" of two magnitudes?
? ? ?
The new theory of proportions
That magnitudes can be incommensurable completely upsets the theory
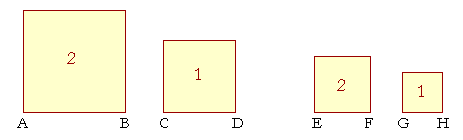
of proportions. For if the square on AB is twice the square on CD, if they are in the ratio 2 : 1, then the lengths AB, CD are incommensurable; 2 is not a square number. And if the square on EF is also twice the square on GH, then EF, GH are also incommensurable -- yet we expect that whatever ratio AB has to CD, EF will have it to GH. We expect, proportionally,
AB is to CD in the same ratio as EF is to GH.
But according to the definition of natural numbers being "in the same ratio," that
will make no sense, because AB is not any multiple of CD, any part of it or any parts of it![]()
Yet we can see that they have the same relationship. Therefore we must create a new definition of "in the same ratio," one that will be applicable to incommensurable magnitudes. We will not present the new definition here. Seeing the need for it -- namely the discovery of incommensurables -- is the climax of our present study. Seeing the need for a new definition of "in the same ratio" was mathematics first logical crisis, and it has always marked the beginning of advanced mathematics.
Next Topic: Irrational numbers
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2020 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
