7
RATIONAL NUMBERS
THE RATIONAL NUMBERS are the numbers of arithmetic. They are the whole numbers, the fractions, the mixed numbers, and the decimals. They are the numbers with whose names and symbols we count and measure.
| 1 5 | 3 8 |
6¼ | .005 9.2 1.6340812437 |
Now we can write any number of arithmetic as a fraction. A whole number, such as 6, we can write as ![]() ; we can write any mixed number as a fraction; and we can write any decimal as a fraction.
; we can write any mixed number as a fraction; and we can write any decimal as a fraction.
We have seen that every fraction has the same ratio to 1 as the numerator has to the denominator:
| a b |
: 1 = a : b. |
A number that has the same ratio to 1 as two natural numbers -- a relationship that we can always name -- we say is rational.
That is why the numbers of arithmetic are called the rational numbers.
(In algebra, those numbers of arithmetic are extended to their negative images. See Topic 2 of Precalculus.)
Problem 1. Which of these numbers are rational?
| 1 5 | 3 8 |
6¼ | .005 9.2 1.6340812437 |
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
All of them.
Problem 2. Write each of the following as a fraction.
| 5 = | 5 1 |
6¼ = | 25 4 |
.35 = | 35 100 |
9.2 = | 92 10 |
1.732 = | 1732 1000 |
Problem 3. To what does the word "rational" refer?
The ratio of two natural numbers.
The number line
![]()
We need the numbers of arithmetic for measuring. Therefore we can think of them as naming a distance from 0 along the number line.
But will those rational numbers account for every distance from 0? Will every length be a rational number of units? To pursue that question, we have the following theorem:
Theorem. Any two rational numbers have the same ratio as two natural numbers.
That is true because:
Fractions with the same denominator have the same ratio
as their numerators.
And we can always express two fractions with the same denominator.
| Example 1. | 2 5 |
: | 3 5 |
= 2 : 3 |
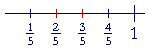
| 2 5 |
is two thirds of | 3 5 |
. |
We could prove that by multiplying both fractions by their common denominator. (Lesson 3.)
| Example 2. | 2 3 |
: | 5 6 |
We can make the denominators the same.
| 2 3 |
= | 4 6 |
Therefore,
| 2 3 |
: | 5 6 |
= | 4 6 |
: | 5 6 |
= | 4 : 5. |
| Example 3. | 2 3 |
: | 5 8 |
In this example, we can choose a common denominator, 3 × 8 = 24. We can then obtain the numerators by cross-multiplying:
![]()
We can always express the ratio of two fractions by cross-multiplying. Cross-multiplying gives the numerators of the common denominator.
| Example 4. | 4 5 |
: | 7 9 |
= | 36 : 35 |
| Example 5. | = | 10 : 3 |
| Example 6. Explicitly, what ratio has | 1 2 |
to 1 | 3 4 |
? |
Explicitly means to verbally name that ratio.
| Answer. | 1 2 |
: 1 | 3 4 |
= | 1 2 |
: | 7 4 |
= 4 : 14 = 2 : 7 |
| Explicitly, then, | 1 2 |
is two sevenths of 1 | 3 4 |
. |
Example 7. .3 is to 1.24 in the same ratio as which two natural numbers?
Answer. We can "clear of decimals" by multiplying both numbers by the same power of 10; in this case, 100:
| .3 : 1.24 | = | 30 : 124 | |
| = | 15 : 62, | ||
| upon dividing by 2. | |||
We have now established the theorem:
Any two rational numbers have the same ratio
as two natural numbers.
Example 8. A photograph measures 2½ inches by 3½ inches. You want to enlarge it so that the shorter side will be 10 inches. How long will the larger side be?
Solution. Proportionally,
| 2½ inches : 3½ inches | = | 5 2 |
: | 7 2 |
= 5 : 7. |
So the question is:
5 : 7 = 10 inches : ? inches
Now, 5 has been multiplied by 2. Therefore, 7 will also be multiplied by 2. (Lesson 3.) The longer side will be 14 inches.
Problem 4. Show that these rational numbers have the same ratio as two natural numbers.
| a) | 5 9 |
: | 7 9 |
= | 5 : 7. The denominators are the same. |
| b) | 15 3 |
: | 16 3 |
= | 15 : 16 | c) | 1 2 |
: | 3 4 |
= | 2 4 |
: | 3 4 |
= 2 : 3 |
| d) | 2 5 |
: | 3 7 |
= | 14 : 15. Cross-multiply. | e) | 1 2 |
: | 1 3 |
= | 3 : 2 |
| f) | 3 8 |
: | 7 10 |
= | 30 : 56 = 15 : 28 | g) | 4 9 |
: | 2 3 |
= | 12 : 18 = 2 : 3 |
| h) | 2 | : | 1 2 |
= | 4 : 1 | i) | 5 6 |
: | 7 | = | 5 : 42 | j) | 2 3 |
: | 1 | = | 2 : 3 | ||
| k) | 1 | : | 1 2 |
= | 2 : 1 | l) | 8 5 |
: | 1 | = | 8 : 5 | m) | 1 | : | 8 5 |
= | 5 : 8 | ||
| n) | 1 : 3 | 1 2 |
= | 1 : | 7 2 |
= 2 : 7 |
| o) | 6 | 7 8 |
: 5 | = | 55 8 |
: 5 = 55 : 40 = 11 : 8 |
| p) | 2 | 3 4 |
: 3 | 1 2 |
= | 11 4 |
: | 7 2 |
= 22 : 28 = 11 : 14 |
Problem 5. Explicitly, what ratio has
| a) | 1 2 |
to 2? | 1 2 |
: 2 = 1 : 4. | 1 2 |
is one fourth of 2. |
| b) | 4 3 |
to | 2 9 |
? | 4 3 |
: | 2 9 |
= 36 : 6 = 6 : 1. | 4 3 |
is six times | 2 9 |
. |
| c) 1 | 1 4 |
to | 1 2 |
? | 1 | 1 4 |
: | 1 2 |
= | 5 4 |
: | 1 2 |
= | 5 4 |
: | 2 4 |
= 5 : 2. | |||
| 1 | 1 4 |
is two and a half times | 1 2 |
. | ||||||||||||||||
Problem 6. Show that these rational numbers have the same ratio as two natural numbers.
| a) | .2 : .3 = 2 : 3 | b) | .2 : .03 = 20 : 3 | c) | 2 : .03 = 200 : 3 |
| d) | .025 : 1 = 25 : 1000 = 1 : 40 | e) | .025 : .01 = 25 : 10 = 5 : 2 |
f) 6.1 : 6.01 = 610 : 601
| Problem 7. A loaf of bread weighs 1 | 1 3 |
pounds, and you |
want to cut off half a pound. Where will you cut the loaf?
| (Hint: What ratio has half a pound to 1 | 1 3 |
pounds?) |
| 1 2 |
: 1 | 1 3 |
= | 1 2 |
: | 4 3 |
= | 3 : 8. Cut three eighths of the loaf. |
Problem 8.
a) Corresponding to every rational number, is there a distance from 0
a) on the number line?
Yes.
b) Corresponding to every distance from 0, is there a rational number?
a)
Hmmm. Is there?
Next Topic: Measurement: Geometry and arithmetic
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2020 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
