Lesson 25 Section 2
SUBTRACTING MIXED NUMBERS
| Example 1. | 8 | 4 5 |
− 1 | 1 5 |
Solution. In this example, we may simply subtract the whole numbers and subtract the fractions -- similarly to adding mixed numbers.
| Example 1. | 8 | 4 5 |
− 1 | 1 5 |
= | 7 | 3 5 |
. |
But consider the following, in which the fractions are reversed:
| Example 1. | 8 | 1 5 |
− 1 | 4 5 |
. |
| How can we deal with that? We cannot take | 4 5 |
from | 1 5 |
. |
To see how to deal with it, consider the following:
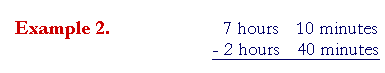
We cannot take 40 minutes from 10 minutes -- we need more minutes. To get them, we will break off 1 of the 7 hours, and decompose it into 60 minutes. We then regroup them with 10 minutes.
60 minutes + 10 minutes = 70 minutes:

2 hours from 6 hours is 4 hours. 40 minutes from 70 minutes is 30 minutes.
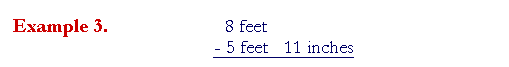
Solution. We cannot take 11 inches from no inches. To make inches, then, from 8 feet we will take 1 foot -- which is 12 inches:
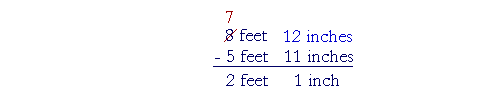
5 feet from 7 feet is 2 feet. 11 inches from 12 inches is 1 inch.
We can now return to our problem:
| 8 | 1 5 |
− 1 | 4 5 |
. |
We need more fifths. Where will we get them? From 8. We will break off 1 from 8, and decompose it into
![]() . (Lesson 21, Example 4.)
. (Lesson 21, Example 4.)
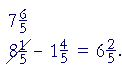
We will then add those ![]() with the original
with the original ![]() making a total of
making a total of ![]() .
.
Then:
| "1 from 7 is 6. | 4 5 |
from | 6 5 |
is | 2 5 |
." |
*
Actually, the simplest way to do this problem is mentally, by rounding off
1![]() to 2. (Compare Lesson 7.) That is, add
to 2. (Compare Lesson 7.) That is, add ![]() to both numbers.
to both numbers.
8![]() − 1
− 1![]() = 8
= 8![]() − 2 = 6
− 2 = 6![]() .
.
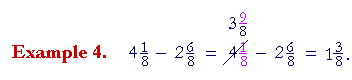
| Break off 1 from 4. Express it as | 8 8 |
, and add it to | 1 8 |
: |
Now the mystery, if any, is: How does that numerator get to be 9?
9 is the sum of the original numerator 1 and denominator 8:

| Example 5. Write the missing numerator: 9 | 2 5 |
= 8 | ? 5 |
| Answer. 8 | 7 5 |
7 is the sum of denominator plus numerator: 5 + 2.
| Example 6. 9 | 2 7 |
− 3 | 5 7 |
= ? |
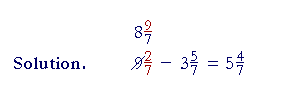
| 9 | 2 7 |
becomes 8 | 9 7 |
. The improper numerator 9 is the sum of the |
| denominator and numerator of | 2 7 |
: 7 + 2 = 9. |
| Example 7. | 6 − 1 | 2 3 |
= | 5 | 3 3 |
− 1 | 2 3 |
| = | 4 | 1 3 |
. | ||||
| "1 from 5 is 4. | 2 3 |
from | 3 3 |
is | 1 3 |
." |
Again, the simplest way to do this is mentally by rounding off 1![]() to 2. Add
to 2. Add ![]() . (Lesson 21.)
. (Lesson 21.)
The problem then becomes
6 − 1![]() = 6
= 6![]() − 2 = 4
− 2 = 4![]() .
.
| Example 8. Prove: 6 − 1 | 2 3 |
= 4 | 1 3 |
Solution. According to the meaning of subtraction,
| 1 | 2 3 |
+ 4 | 1 3 |
= 5 | 3 3 |
= 6. |
Compare Lesson 7, Example 2.
| Example 9. | 6 | 1 2 |
− 2 | 3 4 |
Solution. First, we must make the denominators the same:
| Example 10. | 6 | 1 2 |
− 2 | 3 4 |
= 6 | 2 4 |
− 2 | 3 4 |
We cannot take ![]() from
from ![]() ; therefore, on taking
; therefore, on taking ![]() —1—from 6, the fraction becomes 4-fourths + 2 -fourths = 6-fourths:
—1—from 6, the fraction becomes 4-fourths + 2 -fourths = 6-fourths:
| Example 9. | 6 | 1 2 |
− 2 | 3 4 |
= 5 | 6 4 |
− 2 | 3 4 |
| = 3 | 3 4 |
. | ||||||
| "2 from 5 is 3. | 3 4 |
from | 6 4 |
is | 3 4 |
." |
Mentally:
| 6 | 1 2 |
− 2 | 3 4 |
. | ||
| "3 from 6 | 1 2 |
is 3 | 1 2 |
|||
| Plus | 1 4 |
is 3 | 3 4 |
." | ||
Please "turn" the page and do some Problems.
or
Continue on to the next Lesson.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
