Appendix 3
THEORETIC ARITHMETIC
Triangular numbers
Square numbers
The sum of consecutive cubes
A formula for the triangular numbers
IN THIS TOPIC we will look at numbers themselves, not just their symbols: 1, 2, 3, 4, and so on. By doing so we will see unexpected structures that are inherent in the natural numbers.
Here is a number in the form of a triangle:

This is number 10. (Count them![]() ) Since 10 can be pictured in this way, we call 10 a triangular number.
) Since 10 can be pictured in this way, we call 10 a triangular number.
Now, how do we generate a triangular number? We begin with 1:
![]()
We say that 1 is the first triangular number. To form the next, we add 2:
So the next triangular number is 3. The number we add to the previous triangular number is called the gnomon (NOH-mon). We added the gnomon 2 to 1.
To form the next triangular number, we add the gnomon 3:
![]()
It produces the next triangular number, 6.
To form the next, we add 4:

And so the first four triangular numbers are 1, 3, 6, 10. Each one is the sum of consecutive numbers.
| 1. | ||
| 1 + 2 | = | 3. |
| 1 + 2 + 3 | = | 6. |
| 1 + 2 + 3 + 4 | = | 10. |
Problem 1. Write the first ten triangular numbers.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
1, 3, 6, 10, 15, 21, 28, 36, 45, 55.
The difference between consecutive triangles increases by 1.
A formula for the triangular numbers
We will now show that a triangular number -- the sum of consecutive numbers -- is given by this algebraic formula:
½n(n + 1),
where n is the last number in the sum. (For example, n = 4 in the last sum above.)
To see that, look at this oblong number, in which the base is one more than the height:

An oblong number is the product of a number with its successor, which is the one after. Algebraically, it has the form
n(n + 1).
In this one, the height n is 4; that is, this oblong number is 4 × 5 = 20.
But an oblong is composed of two equal triangles:
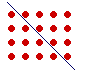
Therefore each triangle is half of the oblong. Each one is
The sum of consecutive numbers is equal to half the product of the
last number in the sum with its successor.
Example. Find the sum of the first 50 numbers -- that is, find the 50th triangular number.
Solution. In the formula, we will put n = 50. Then n + 1 = 51. Therefore the sum is
½(50 × 51) = ½(2550) = 1275.
Problem 2. What is the 200th triangular number?
½(200 × 201) = ½(40,200) = 20,100.
Square numbers

Just as a triangular number is a number that can appear as a triangle, so a square number can take the form of a square. 25 is a square number. If we call 1 the first square number, then by adding which gnomons was 25 produced?
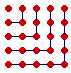
To 1 we added 3 to produce 4.
To 4 we added 5 to produce 9.
To 9 we added 7 to produce 16.
To 16 we added 9 to produce 25.
The gnomons of the squares are the odd numbers.
Every square number is a sum of consecutive odd numbers.
| 1. | ||
| 1 + 3 | = | 4. |
| 1 + 3 + 5 | = | 9. |
| 1 + 3 + 5 + 7 | = | 16. |
| 1 + 3 + 5 + 7 + 9 | = | 25. |
Now, how are square numbers related to triangular numbers?
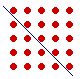
Every square is composed of two consecutive triangles.
Triangles: 1 3 6 10 15 21 28 . . .
| 1 + 3 | = | 4. |
| 3 + 6 | = | 9. |
| 6 + 10 | = | 16. |
| 10 + 15 | = | 25. |
| 15 + 21 | = | 36. |
The sum of consecutive cubes
When the same number is repeated as a factor three times -- as 4 × 4 × 4 -- we call the product the 3rd power of that base; that product is commonly called a cube. (This is analogous to the volume of the solid figure called a cube.)
Here is number 4:
![]()
Upon repeatedly adding it four times --

-- we have the 2nd power, or the square, of 4.
Upon repeatedly adding that power four times --
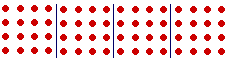
-- we have the 3rd power, or the cube, of 4.
It will be convenient for the moment to express the cube of a number with the exponent 3.
| 13 | = | 1. |
| 23 | = | 8. |
| 33 | = | 27. |
| 43 | = | 64. |
We come now to one of the most remarkable facts in the structure of the natural numbers:
The sum of n consecutive cubes is equal to the square
of the nth triangle.
13 + 23 + 33 + . . . + n3 = (1 + 2 + 3 + . . . + n)2.
To see that, we will begin here:
The difference between the squares of two consecutive triangular numbers
is a cube.
Triangles: 1 3 6 10 15 21 28
| 32 − 12 | = | 23. |
| 62 − 32 | = | 33. |
| 102 − 62 | = | 43. |
| 152 − 102 | = | 53. |
The base of each cube is the difference of the two triangles.
Look -- here is the cube of 4:

From it, let us separate this rectangular array --

-- and reposition it here:

Then we have the square of side 10 --

-- minus the square of side 6![]()
The difference between the squares of those two consecutive triangular numbers is equal to a cube.
Therefore,
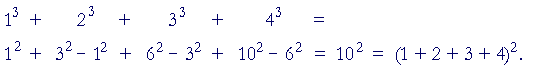
The sum of those four cubes is equal to the square of the fourth triangle.
*
Alternatively, since every square number is the sum of consecutive odd numbers, so is the square of a triangular number.
| 12 | = | 1 |
| (1 + 2)2 | = | 1 + 3 + 5 = 9 |
| (1 + 2 + 3)2 | = | 1 + 3 + 5 + 7 + 9 + 11 = 36 |
| (1 + 2 + 3 + 4)2 | = | 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = 100 |
Therefore, the difference of those squares -- each cube -- will also be the sum of consecutive odd numbers, although not starting with 1.
| 1 | = | 1 |
| 8 | = | 3 + 5 |
| 27 | = | 7 + 9 + 11 |
| 64 | = | 13 + 15 + 17 + 19 |
Again, the sum of those four cubes is equal to the square of the fourth triangle.
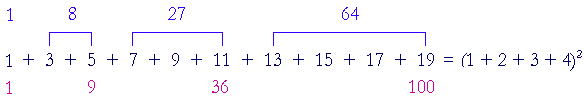
We proved that by mathematical induction
in Topic 27 of Precalculus.
![]()
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
