S k i l l
 i n
A R I T H M E T I C

Table of Contents | Home | Introduction

Lesson 24  Section 2

FRACTIONS INTO DECIMALS

Exact versus inexact decimals

Back to Section 1

In the previous section we saw the most frequent
and therefore the most important decimal and percent equivalents. Nevertheless, we now ask the following:
 3.   What is a general method for changing a fraction to a decimal?
 4 
11
 
  Divide the numerator by the denominator.
 

  Example 1.   Write   4 
11		  as a decimal. 
  Solution.     4 
11		  = 4 ÷ 11.  As they said in the Little Red School House,

"Let 4 fall into the house"

11 does not go into 4.  Write 0 in the quotient, place a decimal point,

and add a 0 onto the dividend. (Lesson 12)

"11 goes into 40 three (3) times (33) with 7 left over.

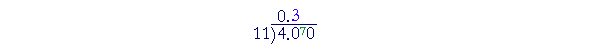
"11 goes into 70 six (6) times (66) with 4 left over."

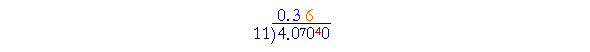
Since we are dividing 11 into 40 again, we see that this division will never be exact.  We will have 36 repeated as a pattern:

 
 4 
11		 = 0.363636. . .
  By writing three dots (called ellipsis), we mean, "No decimal for   4 
11

will ever be complete or exact.  However we can approximate it with as many decimal digits as we please according to the indicated pattern; and

  the more decimal digits we write, the closer we will be to   4 
11		 ."

That explanation is an example of mathematical positivism. It asserts that in the mathematics of computation and measurement, what exists is what we actually observe or name, now. That 0.363636 never ends is a doctrine that need not concern us because it serves no useful purpose. Such actual infinities have no practical effect on calculations in arithmetic or calculus.

What is more, if the decimal really did not end, it would not be a number. Why not? Because a decimal, to be useful, has a name. It is not that we will never finish naming an infinite sequence of digits. We cannot even begin.

  And so we cannot express   4 
11		  exactly as a decimal.  Therefore if we

want to use that number as a decimal, we must approximate it.  Let us approximate it with three decimal digits (Lesson 12):

 4 
11		 0.364
  Example 2.   Write 5  4 
11		  as a decimal. 

Answer.  According to what we just saw:

5  4 
11		 5.364  

Exact versus inexact decimals

  We say then that any decimal for   4 
11		  is inexact.  But the decimal for ¼,

which is .25, is exact.

The decimal  .363636  in and of itself is exact. But
as a value for   4 
11		 , it is inexact.

Fractions, then, when expressed as decimals, will be either exact or inexact.  Inexact decimals nevertheless exhibit a pattern of digits.  The

  pattern for   4 
11		  is .3636363636.

Which fractions -- in lowest terms -- will have exact decimals?  Only those in which the factors of the denominator are 2's and/or 5's.  For it will be possible to multiply only such denominators so that they become a power of 10 -- which are the denominators that a decimal fraction is understood to have.  2's and 5's are the factors of powers of 10.

Here are a few of the numbers that are composed only of 2's or 5's:
2, 4, 5, 8, 10, 16, 20, 25, 40, 50, 250, 400.  A fraction with any of those denominators will have an exact decimal.

A fraction in lowest terms with denominator 6 will not have an exact decimal, because 6 = 2 × 3.  It is not possible to multiply 2 × 3 so that it becomes a power of 10.

Example 3.

  a)   Show the decimal pattern that  1
9		  generates.

9 goes into 1 zero (0).

9 goes into 10 one (1) time with 1 left over.

Again, 9 goes into 10 one (1) time with 1 left over.

And so on. This division will never be exact -- we will keep getting 1's in the quotient.  

1
9		  = 0.111111. . .
  b)   Use that value for  1
9		  to find the value of   8
9		 .
  Solution.     8
9		  = 8 ×  1
9		   =  8 × 0.111111. . . =  0.8888888. . .
  c)   Round off   8
9		  to three decimal digits.
8
9		 0.889.

See Problem 15 at the end the Lesson.

  Example 4.  Calculator problem.   Write as a decimal:   73
96		 .

Answer.  Divide 73 by 96.  Press

73÷ 96 =

Displayed is

 0.7604166 

Therefore, to three decimal digits,

73
96		 .760

Example 5.   In a class of 52 students, 29 were women.

a)  What fraction were women?

  Answer.  Since 29 out of  52 were women, then  29
52		  were women.

(Lesson 20, Question 10.)

b)  Use a calculator to express that fraction as a decimal.

Answer.  Press

2 9 ÷ 5 2 =

See

 0.5576923 

This is approximately  .558.

c)  What percent were women?

Answer.   To change a number to a percent, multiply it by 100.

.558 = 55.8%

(Lesson 4.)

In summary, look at what we have done:

29 out of  52  =  29
52		  =  29 ÷ 52 .558  =  55.8%

"Out of," with a calculator, always signifies division:  Division of a smaller number by a larger.

We will return to this in Lesson 30.


Please "turn" the page and do some Problems.

or

Continue on to the next Lesson.

Section 1 of this Lesson


Introduction | Home | Table of Contents

Please make a donation to keep TheMathPage online.
Even $1 will help.

Copyright © 2012 Lawrence Spector

Questions or comments?

E-mail:  themathpage@nyc.rr.com