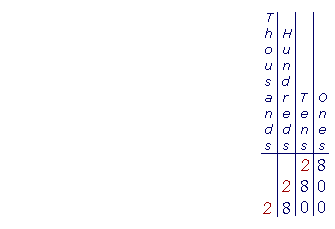Lesson 2 Section 3
MULTIPLYING AND DIVIDING
BY POWERS OF 10
Here is our first example of a problem that not only should not require a calculator. It is a problem you should not even have to write down. It is an example of skill in arithmetic.
| 9. |
How do we multiply a whole number by a power of 10? |
| 28 × 10 | |
| Add on as many 0's as appear in the power. | |
| Example 1. | 28 × 10 | = | 280 | Add on one 0. | |
| 28 × 100 | = | 2800 | Add on two 0's. | ||
| 28 × 1000 | = | 28,000 | Add on three 0's. | ||
We can do that because of our system of positional numeration.
Look at 28 in the figure, and let us push each digit one place left, so that it becomes 280. 280 is then ten times 28 because each digit's place value is now ten times more. (In 28, the '2' tells how many tens, but in 280 it tells how many hundreds.)
Similarly, 2800 = 100 × 28.
Example 2. 608 is 608 ones. How much are 608 tens? 608 hundreds? 608 thousands?
Answers. "608 tens" is 608 × 10. That is the meaning of multiplication (Lesson 9). 608 tens therefore are 6,080. Simply add on a 0.
608 hundreds = 608 × 100 = 60,800. Add on two 0's.
608 thousands = 608 × 1000 = 608,000. Add on three 0's.
Example 3.
a) 50 ones are equal to how many tens?
Answer. 50 ones are simply 50, or 5 tens.
b) 50 tens are how many hundreds?
Answer. 50 tens = 500. (Add on a 0.) 50 tens are 5 hundreds.
c) 50 hundreds are how many thousands?
Answer. 50 hundreds = 5000. (Add on two 0's.) 50 hundreds are 5 thousands.
d) 5000 is how many tens?
Answer. 5000 = 500 × 10. 5000 is 500 tens.
| 10. | When a whole number ends in 0's, how do we divide it by a power of 10? |
| 42,000 ÷ 10 | |
| Take off as many 0's as appear in the power. | |
| Examples. | 42,000 ÷ 10 | = | 4,200 | Take off one 0. |
| 42,000 ÷ 100 | = | 420 | Take off two 0's. | |
| 42,000 ÷ 1000 | = | 42 | Take off three 0's. | |
Problem. Reduce this fraction to its lowest terms:
| 300 500 |
Answer. To reduce a fraction, we must divide both the numerator and denominator by the same number. Now, if a number ends in 0, then we know that it is divisible by 10; while if a number ends in two 0's, we know that it is divisible by 100.
Both 300 and 500 then are divisible by 100:
| 300 500 |
= | 3 5 |
Please "turn" the page and do some Problems.
or
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com