10
SOLVING RIGHT TRIANGLES
This is a topic in traditional trigonometry. It does not come up in calculus.
To SOLVE A TRIANGLE means to know all three sides and all three angles. When we know the ratios of the sides, we use the method of similar figures. That is the method to use when solving an isosceles right triangle or a 30°-60°-90° triangle. When we do not know the ratio numbers, then we must use the Table of ratios. The following example illustrates how.
The general method
Example 1. Given an acute angle and one side. Solve the right triangle ABC if angle A is 36°, and side c is 10 cm.
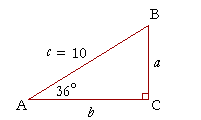
Solution. Since angle A is 36°, then angle B is 90° − 36° = 54°.
To find an unknown side, say a, proceed as follows:
| 1. | Make the unknown side the numerator of a fraction, and make the known side the denominator. |
| Unknown Known |
= | a 10 |
| 2. | Name that function of the angle. |
| Unknown Known |
= | a 10 |
= sin 36° |
| 3. | Use the trigonometric Table to evaluate that function. |
| Unknown Known |
= | a 10 |
= sin 36° = .588 |
| 4. | Solve for the unknown side. |
a = 10 × .588 cm = 5.88 cm
Problem 1. Solve the triangle for side b.
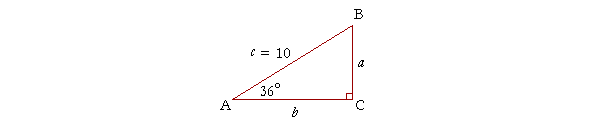
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
To consult the Table, click here.
| Unknown Known |
= | b 10 |
= cos 36° = .809 |
| b | = 10 × .809 = 8.09 cm | ||
Problem 2. To measure the width of a river. Two trees stand opposite one another, at points A and B, on opposite banks of a river.
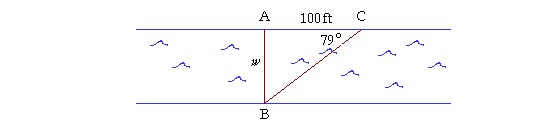
Distance AC along one bank is perpendicular to BA, and is measured to be 100 feet. Angle ACB is measured to be 79°. How far apart are the trees; that is, what is the width w of the river?
| Unknown Known |
= | w 100 |
= | tan 79°. |
| w | = | 100 tan 79° | ||
| = | 100 × 5.145 = 514.5 ft, | |||
from the Table.
(To measure the height of a flagpole, and for the meaning of the angle of elevation, see the Example in Topic 3.)
Example 2. Find the distance of a boat from a lighthouse if the lighthouse is 100 meters tall, and the angle of depression is 6°.
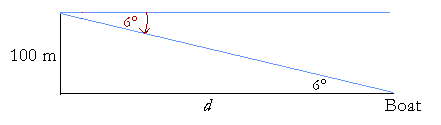
Solution. The angle of depression is the angle below straight ahead -- horizontal -- that an oberver must look in order to see something below the observer. Thus in order to see the boat, the lighthouse keeper must look down 6°.
Now, the triangle formed by the lighthouse and the distance d of the boat from the lighthouse, is right-angled. And since the angle of depression is 6°, then the alternate angle is also 6°. (Euclid, I. 29.)
If d is the distance of a boat from the lighthouse, then
| d 100 |
= | cot 6° | = 9.514, from the Table. |
Therefore,
d = 951.4 meters.
Example 3. Given two sides of a right triangle. Solve the right triangle ABC given that side c = 25 cm and side b = 24 cm.
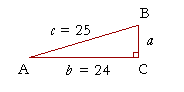
Solution. To find the remaining side a, use the Pythagorean theorem:
| a2 + 242 | = | 252 |
| a2 | = | 625 − 576 = 49 |
| a | = |
Next, to find angle A, we have
| cos A | = | 24 25 |
= | 96 100 |
, |
| on multiplying each term by 4; | |||||
| = | .96 | ||||
(See Skill in Arithmetic: Fractions into decimals.)
We must now inspect the Table to find the angle whose cosine is closest to .96, or, since this is a three place Table, .960.
We find
cos 16° = .961
Therefore,
Angle A ![]() 16°.
16°.
Finally,
Angle B = 90° − 16° = 74°.
We have solved the triangle.
Problem 3. Solve the right triangle ABC given that c = 10 cm and b = 8 cm.
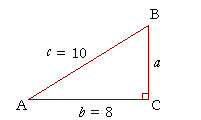
To find the remaining side a, use the Pythagorean theorem:
| a2 + 82 | = 102 |
| a2 | = 100 − 64 = 36 |
| a | = |
To find angle A, we have
| cos A = | 8 10 |
= .8. |
Now inspect the Table to find the angle whose cosine is closest to .8, or, since this is a three place Table, .800.
Find cos 37° = .799.
Therefore,
Angle A![]() 37°. Angle B = 90° − 37° = 53°.
37°. Angle B = 90° − 37° = 53°.
Next Topic: The Law of Cosines
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com