Proof of the sum formulas
| Theorem. | sin ( |
= | sin |
| and | |||
| cos ( |
= | cos |
|
Proof. Let the straight line AB revolve to the point C and sweep out the
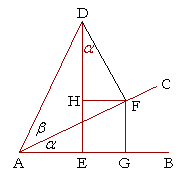
angle ![]() , and let it continue to D and sweep out the angle β;
, and let it continue to D and sweep out the angle β;
draw DE perpendicular to AB.
| Then we are to determine sin ( |
ED DA |
, |
| and cos ( |
AE DA |
. |
Note: The value of a trigonometric function is a number, namely the number that represents the ratio of two lengths. Throughout the proof, then, we will consider AE and DA not only as lengths, but also as the numbers that are their measures. Therefore the usual properties of arithmetic will apply.
Draw DF perpendicular to AC,
draw FG perpendicular to AB,
and draw FH perpendicular to ED.
Then angle HDF is equal to angle ![]() .
.
For, since the straight line AC crosses the parallel lines HF, AB, it makes the alternate angles equal (Theorem 8);
therefore angle HFA is equal to angle ![]() .
.
And by the construction, angle DFH is the complement of angle HFA;
therefore angle HDF (the complement of DFH) is also equal to angle ![]() .
.

Now,
| ED = GF + HD. | ||||||
| Therefore, on dividing by DA, | ||||||
| sin ( |
ED DA |
= | GF DA |
+ | HD DA |
|
And on both dividing and multiplying by AF and FD
| = | GF AF |
AF DA |
+ | HD FD |
FD DA |
Multiplying fractions. |
|
| = | sin |
||||||

Next,
| EA = GA − FH. | |||||
| Therefore, | |||||
| cos ( |
EA AD |
= | GA AD |
− | FH AD |
| = | GA AF |
AF AD |
− | FH DF |
DF AD |
|
| = | cos |
|||||
This is what we wanted to prove.
The difference formulas can be proved from the sum formulas, by replacing +β with +(−β), and using these identities:
cos (−β) = cos β
sin (−β) = −sin β.
Back to Trigonometric identities
Table of Contents | Home
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com