Theoretic Arithmetic
Appendix 3 Section 2
The sum of consecutive cubes
When the same number is repeated as a factor three times -- as 4 × 4 × 4 -- we call the product the 3rd power of that base; that product is commonly called a cube. (This is analogous to the volume of the solid figure called a cube.)
Here is number 4:
![]()
Upon repeatedly adding it four times --

-- we have the 2nd power, or the square, of 4.
Upon repeatedly adding that power four times --
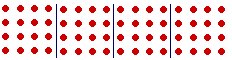
-- we have the 3rd power, or the cube, of 4.
It will be convenient for the moment to express the cube of a number with the exponent 3.
| 13 | = | 1. |
| 23 | = | 8. |
| 33 | = | 27. |
| 43 | = | 64. |
We come now to one of the most remarkable facts in the structure of the natural numbers:
The sum of n consecutive cubes is equal to the square
of the nth triangle.
13 + 23 + 33 + . . . + n3 = (1 + 2 + 3 + . . . + n)2.
To see that, we will begin here:
The difference between the squares of two consecutive triangular numbers
is a cube.
Triangles: 1 3 6 10 15 21 28
| 32 − 12 | = | 23. |
| 62 − 32 | = | 33. |
| 102 − 62 | = | 43. |
| 152 − 102 | = | 53. |
The base of each cube is the difference of the two triangles.
Look -- here is the cube of 4:

From it, let us separate this rectangular array --

-- and reposition it here:
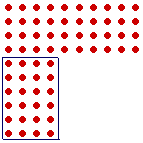
Then we have the square of side 10 --

-- minus the square of side 6.
The difference between the squares of those two consecutive triangles, 10 and 6, is equal to a cube, 43.
Therefore,
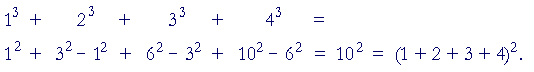
The sum of those four cubes is equal to the square of the fourth triangle.
*
Alternatively, since every square number is the sum of consecutive odd numbers, so is the square of a triangular number.
| 12 | = | 1 |
| (1 + 2)2 | = | 1 + 3 + 5 = 9 |
| (1 + 2 + 3)2 | = | 1 + 3 + 5 + 7 + 9 + 11 = 36 |
| (1 + 2 + 3 + 4)2 | = | 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = 100 |
Therefore, the difference of those squares -- each cube -- will be a sum of consecutive odd numbers, although not starting with 1.
| 1 | = | 1 | ||
| 9 − 1 | = | 8 | = | 3 + 5 |
| 36 − 9 | = | 27 | = | 7 + 9 + 11 |
| 100 − 36 | = | 64 | = | 13 + 15 + 17 + 19 |
Again, the sum of those four cubes is equal to the square of the fourth triangle.
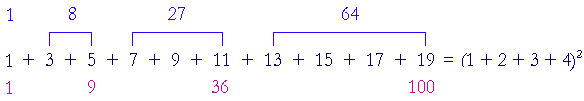
We proved that by mathematical induction
in Topic 27 of Precalculus.
![]()
Introduction | Home | Table of Contents
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
