Lesson 22
EQUIVALENT FRACTIONS
In this Lesson, we will answer the following:
- What are equivalent fractions?
- How can we know when fractions are equivalent?
- How do we convert a fraction to an equivalent fraction with a larger denominator?
- What denominator should we choose
when the denominators of two fractions have no common divisors, and we want to convert them to equivalent fractions with equal denominators? - How do we reduce a fraction to its lowest terms?
- How do we reduce a fraction in which the numerator or denominator is a decimal?
| 1. | What are equivalent fractions? |
| Equivalent fractions have different names but the same value; they are at the same place on the number line. They have the same relationship to 1. | |
Here is an elementary example:
| 1 2 |
= | 2 4 |
. |
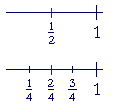
| 1 2 |
is 1 of 2 equal parts of 1. | 2 4 |
is 2 of 4 equal parts. Each |
fraction is one half of 1.
| 2. | How can we know when fractions are equivalent? |
| Both the numerator and denominator of one fraction have been multiplied or divided by the same number. Those products or quotients are the numerator and denominator of the equivalent fraction. | |
| 2 3 |
and | 10 15 |
are equivalent fractions. |
Every fraction has a ratio to 1. Equivlent fractions will have the same ratio to 1.
Since the numerator and denominator are natural numbers, they will have all the properties of ratios, specifically the theorem of the same multiple.
| Example 1. Name three fractions that are equivalent to | 5 6 |
. |
Answer. For example,
| 10 12 |
15 18 |
50 60 |
To create them, we multiplied both 5 and 6 by the same number. First by 2, then by 3, then by 10.
| 3. | How do we convert a fraction to an equivalent fraction with a larger denominator? |
| Multiply the original denominator so that it equals the larger denominator. Multiply the numerator by the same number. | |
| 3 4 |
= | 6 × 3 6 × 4 |
= | 18 24 |
. |
(Compare Lesson 20, Problem 2c.)
Example 2. Write the missing numerator:
| 6 7 |
= | ? 28 |
Answer. To make 7 into 28, we have to multiply it by 4. Therefore, we must also multiply 6 by 4:
| 6 7 |
= | 24
28 |
In practice, to find the multiplier, mentally divide the original denominator into the new denominator, and then multiply the numerator by that quotient. That is, say:
"7 goes into 28 four times. Four times 6 is 24."
Compare Lesson 18, Example 5. Every property of ratios applies to fractions.
Example 3. Write the missing numerator:
| 5 8 |
= | ? 48 |
Answer. "8 goes into 48 six times. Six times 5 is 30."
| 5 8 |
= | 30 48 |
. |
In actual problems, we convert two (or more) fractions so that they have equal denominators. When we do that, it is easy to compare them. Moreover, equal denominators are necessary in order to add or subtract fractions. For we can only add or subtract quantities that have the same name, that is, that are units of the same kind; and it is the denominator of a fraction that names the unit. (Lesson 21.)
Now, since 15, for example, is a multiple of 5, we say that 5 is a divisor of 15.
5 is also a divisor of 20. 5 is a common divisor of 15 and 20.
(15 and 22 have no common divisors, except 1, which is a divisor of every number.)
| 4. | What denominator should we choose when the denominators of two fractions have no common divisors, |
|||
|
||||
| and we want to convert them to equivalent fractions with equal denominators? | ||||
| Choose the product of the denominators. | ||||
Example 4. Convert ![]() and
and ![]() to equivalent fractions with equal denominators.
to equivalent fractions with equal denominators.
Answer. The denominators 3 and 8 have no common divisors (except 1). Therefore, as a common denominator, choose 24.
| 2 3 |
= | 16 24 |
. | 5 8 |
= | 15 24 |
. |
To convert ![]() we said, "3 goes into 24 eight times. Eight tmes 2 is 16."
we said, "3 goes into 24 eight times. Eight tmes 2 is 16."
To convert ![]() we said, "8 goes into 24 three times. Three times 5 is 15."
we said, "8 goes into 24 three times. Three times 5 is 15."
Once we convert to a common denominator, we could then know that ![]() is greater than
is greater than ![]() . Because when fractions have equal denominators, then the larger the numerator, the larger the fraction. (Lesson 20, Question 11.)
. Because when fractions have equal denominators, then the larger the numerator, the larger the fraction. (Lesson 20, Question 11.)
Also, we could now add those fractions:
| 2 3 |
+ | 5 8 |
= | 16 24 |
+ | 15 24 |
= | 31 24 |
. |
See Lesson 21, Example 3.
We can choose the product of denominators even when the denominators have a common divisor. But their product will not then be their lowest common multiple (Lesson 23). The student should prefer the lowest common multiple because smaller numbers make for simpler calculations.
Same ratio
When fractions are equivalent, their numerators and denominators are in the same ratio. That in fact is the best definition of equivalent fractions.
| 1 2 |
= | 2 4 |
. |
1 is half of 2. 2 is half of 4. In fact, any fraction where the numerator is half of the denominator will be equivalent to ![]() .
.
| 1 2 |
= | 2 4 |
= | 3 6 |
= | 5 10 |
= | 8 16 |
. |
1 is half of 2. 2 is half of 4. 3 is half of 6. 5 is half of 10. And so on. They are all at the same place on the number line.
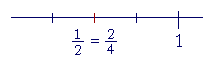
Example 5. ![]() and
and ![]() are equivalent because each numerator is a third of its denominator.
are equivalent because each numerator is a third of its denominator.
Example 6. Write the missing numerator:
| 7 28 |
= | ? 16 |
Answer. 7 is a quarter of 28. And a quarter of 16 is 4.
| 7 28 |
= | 4 16 |
. |
7 is to 28 as 4 is to 16.
| 7 28 |
and | 4 16 |
are equivalent. |
How to simplify, or reduce, a fraction
The numerator and denominator of a fraction are called its terms. To simplify or reduce a fraction means to make the terms smaller numbers. To do that, we divide both terms by a common divisor.
| Example 7. | 24 36 |
= | 24 ÷ 4 36 ÷ 4 |
= | 6 9 |
= | 6 ÷ 3 9 ÷ 3 |
= | 2 3 |
. |
| 24 36 |
, | 6 9 |
, and | 2 3 |
are equivalent fractions. |
Of those three ![]() has the as the lowest terms. We cannot divide any further.
has the as the lowest terms. We cannot divide any further.
We like to express a fraction with its lowest terms because it gives a better sense of its value, and it makes for simpler calculations.
| 5. | How do we reduce a fraction to its lowest terms? |
| Keep dividing both terms by a common divisor. Or, take the same part of both terms. |
|
| Example 8. Reduce to lowest terms: | 15 21 |
. |
Answer. 15 and 21 have a common divisor, 3.
| 15 21 |
= | 5
7 |
Or, take a third of both 15 and 21.
"A third of 15 is 5."
"A third of 21 is 7."
| Example 9. Reduce | 200 1200 |
. |
Answer. When the terms have the same number of 0's, we may ignore them.
| 200 1200 |
= | 1 6 |
Effectively, we have divided 200 and 1200 by 100. (Lesson 2, Question 10.)
| Example 10. Write as a mixed number: | 20 8 |
. |
Solution. Divide 20 by 8. "8 goes into 20 two (2) times (16) with 4 left over."
| 20 8 |
= 2 | 4 8 |
= 2 | 1 2 |
. |
| 4 8 |
is equivalent to | 1 2 |
. |
Or, we could reduce first. 20 and 8 have a common divisor 4:
| 20 8 |
= | 5
2 |
| = | 2½. | |
Notice that we are free to interpret the same symbol
| 20 8 |
| in various ways. It is the fraction | 20 8 |
. It is 20 divided by 8. |
And it indicates "the ratio of 20 to 8."
| Example 11. Reduce | 5 5 |
. |
| Answer. | 5 5 |
= 1. |
Any fraction in which the numerator and denominator are equal, is equal to 1.
| Summary |
 |
At this point, please "turn" the page and do some Problems.
or
Continue on to the next Section.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
